本來以為背背板子就夠用了的，發現有的時候會需要其中的一些東西。

原來樹狀數組也有自己的不可替代性。

但是像用樹狀數組做平衡樹這種我確確實實不感興趣。

當摸魚寫一些吧。

個人認為，樹狀數組是最能體現 OI 魅力的數據結構，它集簡潔，巧妙，智慧與一身，我非常喜歡。

這個是記錄向的，并不是教學向的，就是閑得沒事瞎寫的。

lowbit 函數

如果想要真正理解樹狀數組，我們需要說說這個用途不僅僅限于樹狀數組，還有假壯壓騙分等等用途的 lowbit。

lowbit(x) 表示的是 x 在二進制表示下最低位的 1 和后邊的所有 0 組成的數值。

通過這個我們可以快速鎖定最低位的 1 并簡單的進行這個最低位 1 的刪除，而且這個東西是可以快速求解的。

來說一下我們通常遇見的形式是怎么來的。

我們設一個數二進制表示下第 k 位是 1, 0～k-1 位都是0。

先把這個數字取反，這個時候 0~k-1 的這一堆 0 就變成了 1, 第 k 位就變成了 0,這個時候我們再加一，前邊的一堆 1 都會變成 0,最終這個進位的過程停止在 k 的位置，由于取反現在前邊的位置都是恰好相反的，這個時候我們與原來的數字進行按位與就好了。

補碼之下，取反 x 表示為 -1-x。

所以我們得到了最常見的形式：lowbit(x)=x&(-x);

非常的優美。

一維樹狀數組

這里涉及單點修改區間查詢，區間修改單點查詢，區間修改區間查詢。

我們以最基本的單點修改區間查詢做例子。

單點修改，區間查詢

先給一張藍書的圖片吧，這個就是我們的樹狀數組的樣子了。

注意是別人的圖，我覺得這個圖片棒極了，偷偷貼一下。

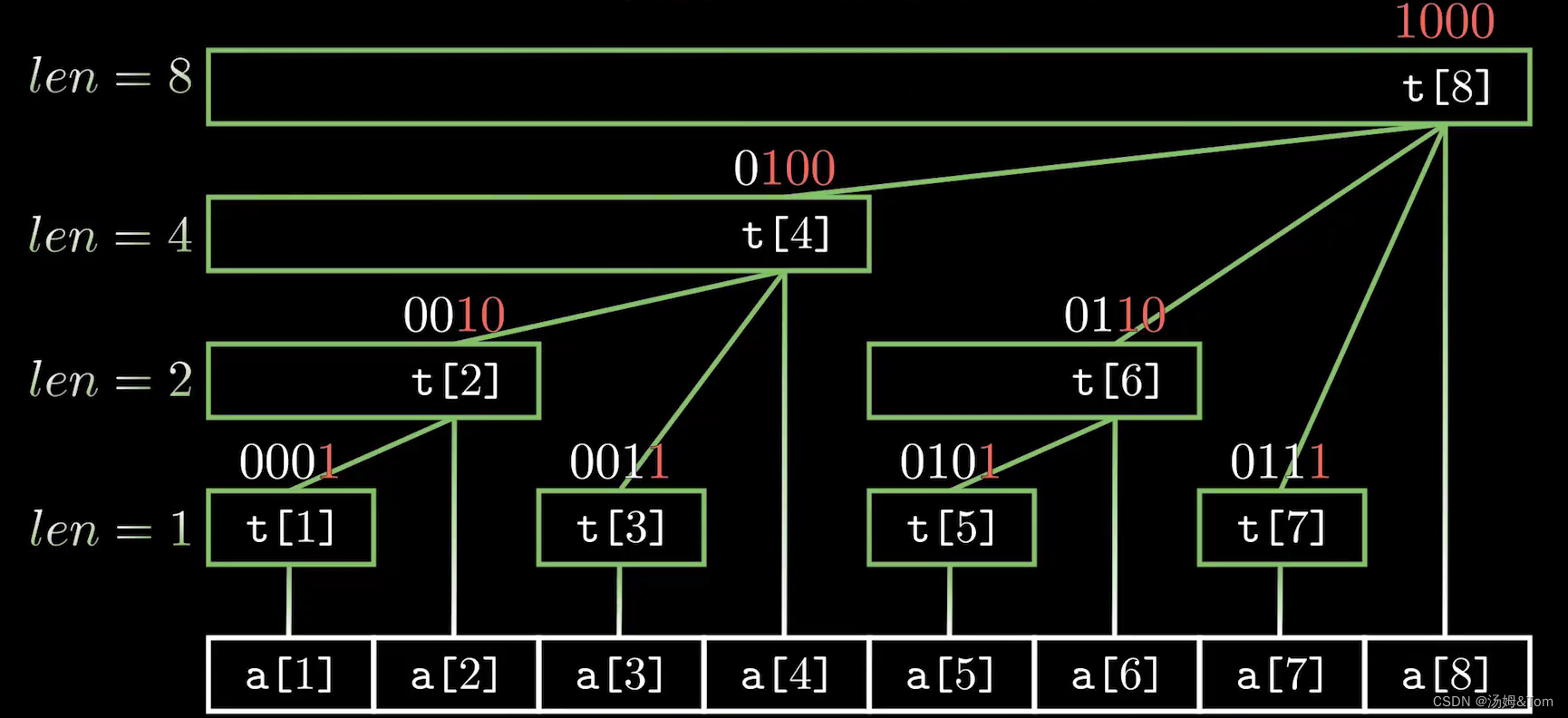
在樹狀數組中，\(tr[i]\) 表示區間 \([i-lowbit(i)+1,x]\) 中的信息并。

以下我們以動態維護單點加減一個數字，區間求和為例子。

這個信息并自然就是區間的和。

先考慮區間求和，先假定左端點是 1。

我們發現區間的左右端點都是數字（廢話）。

而眾所周知，一個數字是可以被二進制分解的（廢話*2）。

所以我們就可以通過二進制分解把這個東西搞成 \(log n\) 段，我們便可以將其對應在樹狀數組的各段上邊。

比如說我們要求 \([1,6]\) 的和，6 的二進制是 110, 我們就可以將其分解成 110 段和 100 段，對應了樹狀數組的 4 和 6,我們在圖上可以明顯感受到這一點。

每一次跳段我們使用 lowbit 函數就行了。

我們發現這個不會大于 \(log\) 次的，跳的次數永遠是二進制表示下 1 的數量，這也是樹狀數組速度極端優秀的根本原因。

如果左端點不是一我們就做差就行了，[a,b]=[1,a-1]-[1,b] 這個樣子把答案差分出來就行了。

但這種查詢方式讓我們只能直接維護可以被差分的信息，大大減少了這個東西的泛用性，比如不能直接維護區間最值（其實可以，但是比較復雜，我不會）。

至于單點的修改，我們發現改一個點只會影響到覆蓋自己的點，我們就不停加自己的 lowbit 就行了，把每個祖先加上自己的值，這個明顯也是 log 級別的。

區間修改，單點查詢

我們使用差分就行了，很簡單，這里不解釋差分了。

依然以加法為例子。

我們把 \([a,b]\) 的加 val 轉化為差分數組中的 d[a] 加上 val，d[b+1] 減去 val 就成為了之前的問題。

求一個點的值自然就是求差分數組的前綴和。

就沒了。

區間修改，區間查詢

我們還是利用前綴和與差分的知識。

我們把區間求和用差分數組列出來，默認從 1 開始了，如上原因，都一樣的。

\(\sum_{x}^{i=1}\sum_{j=1}^{i}d[j]\)

這個玩意難優化，我們考慮每一個 d[j] 出現了多少次，對于一個 j 自然是出現了 (x-j+1) 次的，我們直接改為枚舉 d[j]，通過出現次數來計算，就成了如下形式。

\(\sum_{j=1}^{x}(x-j+1)d[j]\)。

我們發現這樣子依然是十分甚至九分的低效，于是我們開始拆開式子。

\((x+1)\sum_{j=1}^{x}d[j]-\sum_{j=1}^{x}j\times d[j]\)

我們使用兩個樹狀數組分別維護 d[j] 和 d[j]* j 的前綴和就好了。

經典的應用

• 逆序對

• 優化一些過程

• 維護最后的 1

二維樹狀數組

也是一樣的，只不過我們多了一維。