擴展 KMP(Z函數)
集訓的時候講了一下,覺得很有意思,難度也比較小,學 SA 學累了,加上感覺沒太多人寫這個,故有了這篇筆記。
請注意,本文所有的字符串的下標都是從 1 開始的,本人討厭從 0 開始。
請注意,本文所有的字符串的下標都是從 1 開始的,本人討厭從 0 開始。
請注意,本文所有的字符串的下標都是從 1 開始的,本人討厭從 0 開始。
重要的話說三遍。
介紹
擴展 KMP 聽起來像是和 KMP 有很大聯系,其實他們一點關系都沒有,反倒和 Manacher 的思想差不多,這個東西也叫 Z 函數,顧名思義,這個算法就是在求一個函數。
我們定義的一個函數 \(z[i]\),這個函數表示對于整個字符串和從 \(i\) 開始向后截取的字符串,兩個字符串的最長公共前綴的長度。
舉個例子:我們有個字符串 abbaabbca。
\(z[5]=3\),因為顯然最長公共前綴是 abb。
我們管這個叫 LCP。
我們需要做的就是在 \(O(n)\) 求出來每個位置的函數值。
所以往后本文會同時使用 Z 函數與擴展 KMP 兩個名字,前者就指這個函數。
算法流程
似乎不太好做,考慮從左往右求解。
我們發現如果之前有一個最長公共前綴覆蓋了我們正在求的位置,我們似乎可以繼承曾經的值誒。
我們決定順著這個思路去想。
畫一個圖先感性看一下,之后再去分析細節。
建議讀圖順序:黃綠藍紅。
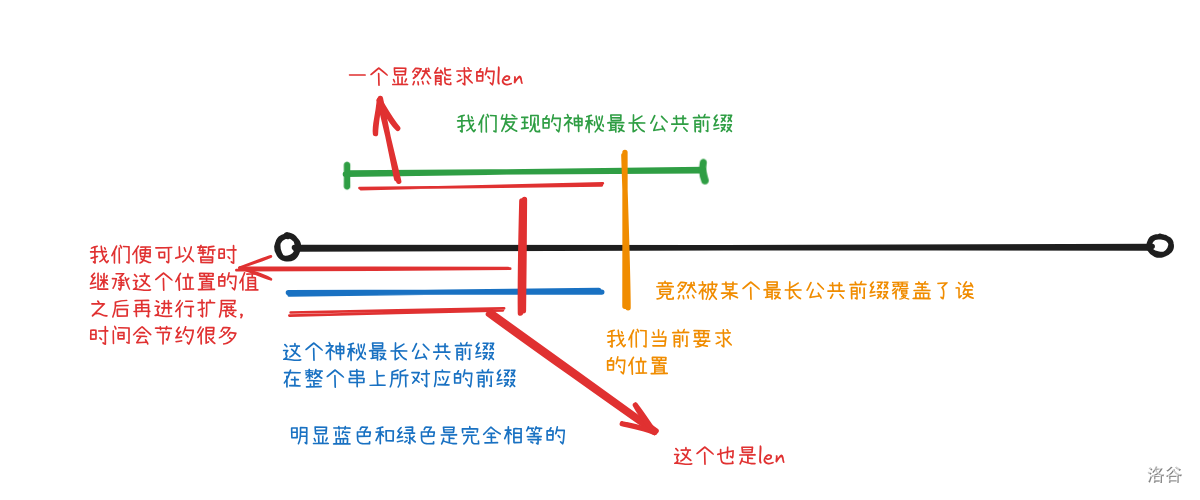
如果有一個我們維護的最長公共前綴覆蓋了我們當前要求的點,我們就可以通過所記錄這個最長公共前綴的起點和終點推算出我們可以繼承前邊已經求過的哪個點了。
按著這個思路我們來設計一下算法。
我們一共有三個步驟:繼承,擴展,維護盒子。
我們管我們維護的,前邊出現的最長公共前綴叫做加速盒子,因為我們是依據它才能加速我們的求解的。
請記住我們名稱的轉變。
所以我之后就管這個叫盒子了。
我們在外部維護兩個變量 \(l\) 和 \(r\),它們表示盒子的左端點和右端點。
繼承
首先我們需要考慮的就是繼承的問題,想上圖一樣繼承前邊的值來加速。
假設我們現在求的位置為 \(i\),按照我們上邊圖片的思路,如果這個點被我們的盒子覆蓋了,我們該繼承哪一個呢?
先把上圖的 \(len\) 求出來,明顯就是 \(i-l+1\)。
那么我們就繼承 \(z[i-l+1]\) 的值。
但這樣還有一個問題,那就是我們不能保證我們繼承的值完全合法。
我們僅僅可以保證盒子內是一樣的,但是盒子外是未知的,這個盒子不一定完全記錄了 \(i-l+1\) 的信息,中途可能更新了別的信息。
所以如果這個繼承的點的值過大超出了我們盒子的范圍,我們就沒有辦法保證正確了。
解決辦法很簡單,我們給這個點可能的最大值限制成它到右端點的距離就行了,保證不會超出。
人話:對 \(r-i+1\) 取 min。
所以我們對于繼承的式子就出來了,如果 \(i\le r\) 的話:\(z[i]=min(z[i-l+1],r-i+1)\)。
一定不要忘記判斷 \(i\le r\),我有的時候打代碼打爽了比較快會忘了這個判斷。
擴展
所謂擴展,就是暴力擴展。
沒有開玩笑,就是一個一個跳。
\(n\) 代表整個字符串長度,同時 \(s\) 代表字符串。
在保證 \(i+z[i]\le n\) 的情況下,我們使用一個循環判斷 \(s[i+z[i]]=s[1+z[i]]\) 是否成立,也就是暴力。
每次成立我們直接將 \(z[i]\) 加一就行了。
為什么是對的我們之后再講。
維護盒子
現在我們的 \(z[i]\) 是沒有參雜一點水分的,最終形態的 \(z[i]\) 了。
但是吃水不忘挖井人,我們需要時刻維護盒子,讓后邊的位置享受到加速盒子的美好。
也很簡單,我們判斷以下當前最長公共前綴有沒有延伸出盒子,前邊不是暴力擴展了嗎,如果伸出來了,我們將盒子左端設為當前位置,右端點設為所延伸的地方。
形式化一些,如果我們發現 \(i+z[i]-1 > r\),我們就直接將 \(l\) 設為 \(i\),\(r\) 設為 \(i+z[i]-1\)。
于是就沒有了,你聽懂了嘛。
時間復雜度
沒學過 Manacher 的就會問了:主播主播,你的算法確實很強,但憑什么說這個就是 \(O(n)\) 的?這不也有暴力嗎?
BaiBaiShaFeng 會告訴他這個絕對不是瞎說的。
我們會發現整個過程中 \(r\) 都是單調不減的。
而我們在 \(r\) 以內的都可以直接轉移過來,而 \(r\) 最多跳 \(n\) 次。
所以是 \(O(n)\) 的。
如果還是不明白?
想象以下你正在寫 \(n\) 道題,中途隨時可能需要回 npy 的 \(n\) 條消息,你最后會操作 \(2n\) 次,這下就明顯了吧。
代碼
都說到這個份上了,隨便放一下應該都能看懂了吧。
void Z_func(string s){
int n=s.size()-1; z[1]=n;//設置初始值
for(int i=2,l=1,r=1; i<=n; ++i){
if(i<=r) z[i]=min(r-i+1,z[i-l+1]);//繼承
while(i+z[i]<=n&&s[i+z[i]]==s[1+z[i]]) ++z[i];//擴展
if(i+z[i]-1>r){
l=i; r=i+z[i]-1;//維護盒子
}
}
}
例題
P5410 【模板】擴展 KMP/exKMP(Z 函數)
給你兩個字符串,分別是 \(a\) 和 \(b\)。我們首先要求出來 \(b\) 的 Z 函數,然后求出來 \(b\) 和 \(a\) 的每個后綴的 LCP。
需要 \(O(n)\) 的時間復雜度。
最后有輸出格式要求,我們這里忽略不計了。
問題一很好求,就是之前的那個,我們思考以下怎么求問題二。
這個其實利用 Z 函數就行了。
我們將 \(a\) 拼接到 \(b\) 的右邊,在兩個串中間加入一個特殊符號做分割,我們在這個串上再做一次擴展 KMP。
統計的時候,我們在 \(b\) 的范圍中統計,看一下在 \(a\) 中對應哪個位置,也就是 \(m+2+i-1\),別忘了中間還有一個分割符號,得到 \(z[n+2+i-1]\),再對 \(m\) 取 min 保證能被放到 \(b\) 中就行了。
放一下代碼↓
#include <bits/stdc++.h>
using namespace std;
const int MN=4e7+217;
int zb[MN], zc[MN];
void Z_funcb(string s){
int n=s.size()-1; zb[1]=n;
for(int i=2,l=1,r=1; i<=n; ++i){
if(i<=r) zb[i]=min(r-i+1,zb[i-l+1]);
while(i+zb[i]<=n&&s[i+zb[i]]==s[1+zb[i]]) ++zb[i];
if(i+zb[i]-1>r){
l=i; r=i+zb[i]-1;
}
}
}
void Z_funcc(string s){
int n=s.size()-1; zc[1]=n;
for(int i=2,l=1,r=1; i<=n; ++i){
if(i<=r) zc[i]=min(r-i+1,zc[i-l+1]);
while(i+zc[i]<=n&&s[i+zc[i]]==s[1+zc[i]]) ++zc[i];
if(i+zc[i]-1>r){
l=i; r=i+zc[i]-1;
}
}
}
string a, b, s;
int main(){
ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
cin>>a>>b; int n=a.size(), m=b.size(); a=' '+a; b=' '+b;
s=" "+b.substr(1)+"|"+a.substr(1); Z_funcb(b); Z_funcc(s);
long long res=0;
for(int i=1; i<=m; ++i) res^=(long long)1*(i)*(zb[i]+1);
long long ans=0;
for(int i=1; i<=n; ++i){
int p=zc[m+2+i-1]; p=min(p,m);
ans^=(long long)1*(i)*(p+1);
}
cout<<res<<'\n'<<ans<<'\n';
return 0;
}
CF432D Prefixes and Suffixes
給你一個字符串 \(s\),定義一個完美子串為一個同時是 \(s\) 的前綴和后綴的子串,需要統計有幾個這樣的子串并統計每個在這個串中的出現次數。
這里的 \(\left | s\right | \le 10^5\)。
我們發現統計有幾個這樣的子串是很簡單的,只需要使用 KMP 的 nxt 數組,從 \(nxt[n]\) 開始不停跳 nxt 就行了。
來學這個的想必都對 KMP 這種基礎一些的東西很了解了。
我們其實只需要統計一定長度的前綴在串中出現了多少次。
這個東西是可以使用擴展 KMP 做的,我們維護每個長度的前綴在串中出現的次數,對于位置 \(i\),我們將它視為一個子串的左端點,發現它可以貢獻 \([1,z[i]]\) 長度的前綴數量,我們直接將這個區間的數量加一就行。
這個可以 \(O(n)\) 差分的,但是我喜歡樹狀數組,反正數據范圍小,具體維護無所謂啦。
代碼↓
#include <bits/stdc++.h>
using namespace std;
const int MN=1e6+116;
string s; int n, z[MN], nxt[MN];
struct BIT{
int tr[MN], n;
void init(int _n){
n=_n; memset(tr,0,sizeof(tr));
}
int lowbit(int x){
return x&(-x);
}
void update(int pos, int val){
for(int i=pos; i<=n; i+=lowbit(i)) tr[i]+=val;
}
void update_range(int l, int r, int val){
update(l,val); update(r+1,-val);
}
int qval(int pos){
int res=0; for(int i=pos; i; i-=lowbit(i)) res+=tr[i];
return res;
}
}bit;
vector <pair<int,int>> qry;
int main(){
ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
cin>>s; n=s.size(); s=' '+s; z[1]=n; bit.init(n);
for(int i=2,l=1,r=1; i<=n; ++i){
if(i<=r) z[i]=min(r-i+1,z[i-l+1]);
while(i+z[i]<=n&&s[i+z[i]]==s[1+z[i]]) ++z[i];
if(i+z[i]-1>r){l=i; r=i+z[i]-1;}
}
int j=0; nxt[1]=0;
for(int i=2; i<=n; ++i){
while(j&&s[j+1]!=s[i]) j=nxt[j];
if(s[j+1]==s[i]) j++; nxt[i]=j;
}
for(int i=2; i<=n; ++i){
if(z[i]) bit.update_range(1,z[i],1);
}
int pos=n;
while(pos>0){
qry.push_back({pos,bit.qval(pos)+1});
pos=nxt[pos];
}
reverse(qry.begin(),qry.end());
cout<<qry.size()<<'\n';
for(auto v:qry){
cout<<v.first<<" "<<v.second<<'\n';
}
return 0;
}
一些擴展 KMP 也可以干的事情
這里收回我之前說的話,其實兩個算法還是有共同點的,有一些 KMP 可以干的事情我們的擴展 KMP 同樣可以干,個人認為這一塊沒什么大用,能用 KMP 為啥不用,但對于掌握擴展 KMP 還是有一定用途的,再說了 OI Wiki 都放了。
匹配子串
這是 KMP 可以做的那個模式串與文本串的匹配,我們只能搞最長公共前綴,想要匹配怎么辦。
這個簡單,我們把模式串拼到文本串之前,再向中間加一個特殊的分隔符,這樣再跑擴展 KMP,我們會發現在這上邊我們就可以匹配了。
我們只需要看看后邊屬于文本串的函數值有沒有達到模式串的長度,這個正確性是比較好想的,我就不展開講了,實在不懂畫個圖。
下邊是 A 掉 KMP 模板的代碼,匹配子串不需要 nxt 數組,只是題目需要輸出 nxt 數組而已。
代碼↓
#include <bits/stdc++.h>
using namespace std;
const int MN=2e7+117;
string s, t, str;
int z[MN], n, nxt[MN];
int main(){
ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
cin>>s>>t; str=t+'#'+s; n=str.size();
str=' '+str; z[1]=n;
for(int i=2,l=1,r=1; i<=n; ++i){
if(i<=r) z[i]=min(r-i+1,z[i-l+1]);
while(i+z[i]<=n&&str[i+z[i]]==str[1+z[i]]) ++z[i];
if(i+z[i]-1>r){l=i; r=i+z[i]-1;}
}
int m=t.size(), j=0; t=' '+t; nxt[1]=0;
for(int i=2; i<=m; ++i){
while(j&&t[j+1]!=t[i]) j=nxt[j];
if(t[j+1]==t[i]) ++j;
nxt[i]=j;
}
for(int i=m+1; i<=n; ++i){
if(z[i]==m){
cout<<i-m-1<<'\n';
}
}
for(int i=1; i<=m; ++i) cout<<nxt[i]<<" ";
}
本質不同子串數量
這個應該可以使用 SA 或者 SAM, 都可以 \(O(n)\) 來做,而如果使用 Z 函數就是 \(O(n^2)\) 的,所以這個大概沒什么用,不給代碼了。
考慮已經知道了串 \(s\) 的本質不同的子串數量,現在插入一個字符,計算數量的變化情況。
我們可以將 \(s\) 與后邊加上的字符看作串 \(s'\),對 \(s'\) 進行一下翻轉,我們對這個 \(s'\) 去求 Z 函數。
我們將這個問題轉化為了一個前綴的問題,我們新增了一些以新字符打頭的前綴,現在我們想知道在整個串中有多少串是沒有出現過的。
這個并不難做,我們找出跑出來的 Z 函數的最大值,這個就是在串中出現過的最長前綴,同時說明比它小的前綴同樣出現了。
所以每次的貢獻就是 \(\left | s'\right |-z_{max}\)。
于是我們就會做了。
如果問題改為在端點添加或者刪除一個字符,讓你統計我們就是 \(O(n)\) 的了,萬一用得上呢。
求解字符串整周期
就是找一個最小的字符串 \(t\),使得整個串被這個 \(t\) 所拼接表示。
沒錯,這個就是能 KMP 做,但是我們現在要使用今天的東西。
我們直接尋找最小的 \(i\) 滿足 \(i+z[i]=n\)。
直觀的,對于滿足這樣的一個 \(i\),它的前綴是 \(n-i\),也就是可以覆蓋整個字符串,正確性同 KMP 的證明。
需要特別注意:如果要求整周期,需要保證 \(i\) 是 \(n\) 的因數,而如果只是求解最短循環節就不需要這個限制。
結語
寫了這么久也累了,總結以下這片筆記的內容吧。
擴展 KMP,又稱 Z 函數,是一個直接用于解決最長公共前綴的字符串算法,衍生出一些用法,與 KMP 有重疊,但對于各點與整串的前綴處理方面有獨到的作用。
這個算法的題目還是比較少的,所以沒有太多的例題,我做過的除例題外的這類題都放到下邊了。
本文參考了 OI-Wiki,主要參考了擴展 KMP 的應用,也是為了更好的總結。
如果本文有任何的問題,錯誤,不足或者模糊的地方,歡迎各位進行指正,如果有好的題目也可以分享一下,如果有空會將一些好題加入這篇文章。
最后的,祝福大家 OI 學習開心,也紀念本人學習 OI 的一周年。
一些題目
CF1968G2 Division + LCP (hard version)


 浙公網安備 33010602011771號
浙公網安備 33010602011771號