Manacher

注:全文字符串下標自 \(1\) 開始

呃......

眾所周知, 在 \(NOI2025\) 大綱中這個玩意已經屬于提高組了

對于任何字符串不會的我真的是太可怕了, 所以連夜補習終于學會馬拉車

做個小整理, 不知道為什么覺得今年剛加進來說不定會考......

---

What is Manacher?

Manacher是一個用來求解字符串中每個位置的最長回文半徑的算法

它的時間復雜度也很優秀, 是可愛的 \(O(n)\)

而且代碼實現極其簡單, 水題時很爽.

先給一下原理, 隨便講講

---

How Can I Do My Manacher

奇偶化一

我們發現回文子串有一個很惡心的點: 它的長度有的是奇數, 有的是偶數

其它問題還好說, 但現在我們要干的是求長度, 每次考慮中間會讓我說出及其惡毒的語言

所以我們使用一個操作: 將每個字符之間插入一個奇怪的字符(不是原字符串中出現的)

舉個例子

原串: ABCBABA

我們轉化成: #-A-B-C-B-A-B-A-

為什么要最左邊的奇怪字符呢?

呃......我們后邊需要對回文半徑進行暴力擴展, 放一個防止越界

如此一來, 我們便將所有的子串轉化成奇數

---

怎么個事

我們先設回文半徑為 \(d[i]\) 方便我們表示

如果我們一個一個去暴力求解, 我們會得到 \(O(n^2)\) , 沒錯你的好朋友 \(O(n^2)\)

這個復雜度讓 \(CCF\) 看了都流淚, 連夜整出一堆很水的數據讓你通過

我們可以類比其他字符串算法的思想

---

現在我們已經求出來了 \([1,i-1]\) 內所有的 \(d\)

我們尋找有無辦法迅速推出現在的 \(d[i]\)

類比擴展KMP(這個都會吧...不會也沒有關系), 我們可以整一個加速的盒子

"盒子"是什么?

在Manacher中, 我們需要維護一個最長的回文子串, 這樣在推下一個位置的時候我們可以通過回文子串的性質強硬使用對稱減少無用的擴展

具體如下圖

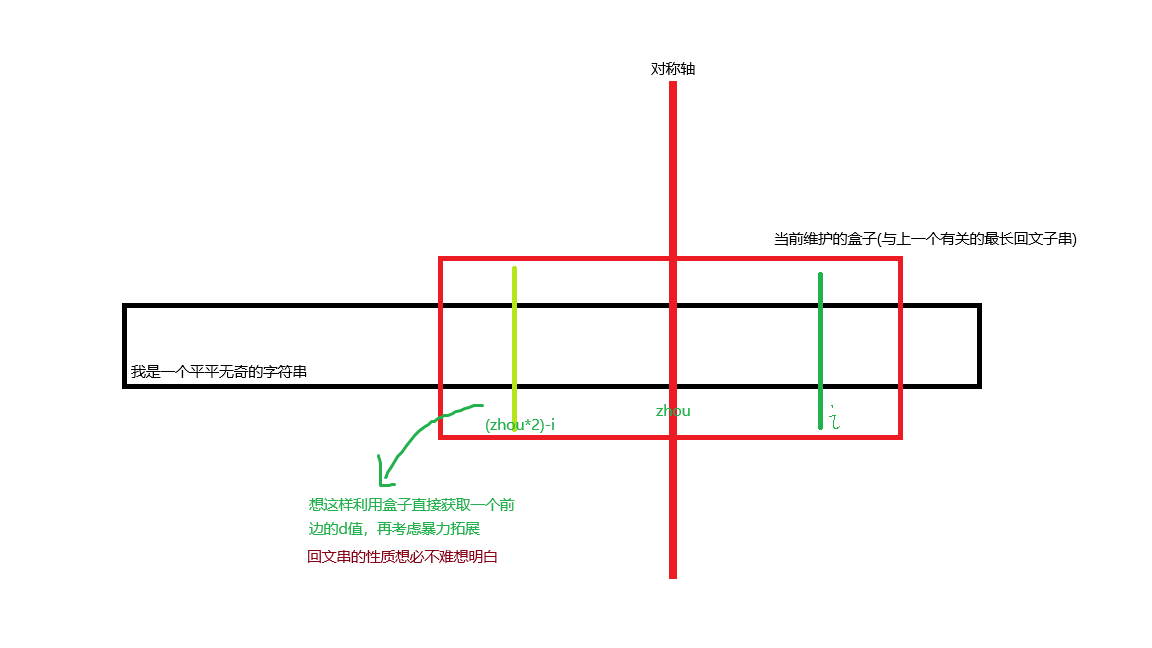
我們直接繼承 \(d[i]\) 為 \(min(d[(zhou*2)-i], r-i+1)\)

\(r\) 所代表的是盒子的右端點, 取最小值保證在盒子內

---

之后我們一直暴力擴展, 如果 \(s[i+d[i]]=s[i-d[i]]\) , 我們就直接將 \(d[i]\) 加一, 直到無法暴力擴展

最后我們再進行判斷這個盒子可不可以暴力拓展

具體來說:

判斷一下 \(i+d[i]-1>=r\) 嗎?

如果大于, 我們便將 \(r\) 設為 \(i+d[i]-1\)

將軸設為 \(i\)

這樣就結束了(本人喜歡在代碼中把判斷寫成\(i+d[i]>r\))

---

Why \(O(n)\) ?

有人會問: 都暴力擴展了辣么多次, 你憑什么說這個是線性的? 我不信.

這個的解釋跟擴展KMP也特別像(憑啥要叫擴展KMP啊喂)

這個其實很好想, 我們每次暴力擴展中都會增加 \(r\), 而這個 \(r\) 是只升不降的, 在 \(r\) 內的我們又可以直接推得

所以我們暴力擴展其實是 \(O(n)\) 的.

就這么簡單, 沒想到吧

給一下代碼:

模板: Manacher 模板

#include <bits/stdc++.h>
using namespace std;
const int MN=3e7+317;
char s[MN];
int ans=0, d[MN], length=1;
void Read(){
    char r=getchar(); s[0]='$'; s[length]='-';
    while(r>='a'&&r<='z'){
        s[++length]=r;
        s[++length]='-';
        r=getchar();
    }
    s[length]='-';
}
void Manacher(){
    for(int i=1,j=0,zhou=0; i<=length; ++i){
        d[i]=min(d[(zhou<<1)-i],j-i+1);
        while(s[i+d[i]]==s[i-d[i]]) d[i]++;
        if(i+d[i]>j){
            j=i+d[i]-1;
            zhou=i;
        }
        ans=max(ans,d[i]);
    }
}
int main(){
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    Read(); Manacher(); cout<<ans-1<<'\n';
    return 0;
}

和 \(wyx\) 一樣短小精悍

---

---

有趣的題目

隨便給一些

國集:拉拉隊排練

題意簡述

給定一個長度為 n 的小寫字母字符串，統計所有長度為奇數的回文子串。
將這些回文子串按長度降序排序，取前 K 個長度的乘積（模 19930726）。若總數不足 K 個，輸出 -1。

就直接去跑 \(Manacher\), 跑完了把非插入符的回文半徑存一下(這個就是字串長度,有插入符)

#include
#define int long long
using namespace std;
const int MN=2e6+316;
const int mod=19930726;
int n, k, d[MN], length=1;
int cnt[MN], sum=0, ans=1;
string str; char s[MN];
void Read(){
    s[0]='%', s[length]='-';
    for(auto c:str){
        s[++length]=c;
        s[++length]='-';
    }
    s[length]='-';
} 
void Manacher(){
    for(int i=1,j=0,zhou=0; i<=length; ++i){
        d[i]=min(d[(zhou<<1)-i],j-i+1);
        while(s[i+d[i]]==s[i-d[i]]) d[i]++;
        if(i+d[i]>j){
            j=i+d[i]-1;
            zhou=i;
        }
        if((d[i]-1)%2) cnt[d[i]-1]++;
    }
}
int quick_power(int a, int b){
    int res=1;
    while(b){
        if(b&1){
            res=(res*a)%mod;
        }
        a=(a*a)%mod;
        b>>=1;
    }
    return res;
}
signed main(){
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    cin>>n>>k>>str; Read(); Manacher(); n=length;
    for(int i=n; i>=1; --i){
        if(i%2==0) continue;
        sum+=cnt[i];
        int use=min(k, sum);
        ans=(ans * quick_power(i, use)) % mod;
        k-=use;
        if(k<=0) break;
    }
    if(k>0) ans=-1;
    cout<<ans<<'\n';
    return 0;
}

這個就沒啦

綠綠和串串

題意簡述
給定字符串 \(S\)，求所有可能的初始串 \(R\) 的長度（\(|R| \leq |S|\)），使得 \(R\) 經過若干次翻轉操作后得到的串以 \(S\) 為前綴。

翻轉操作定義：每次操作將前 \(|R|-1\) 個字符倒序拼接到 \(R\) 末尾（例如 abcd → abcdcba）。

數據范圍：\(|S| \leq 10^6\)，總 \(\sum |S| \leq 5 \times 10^6\)。

我們要多動手, 手摸一下?

發現想要能換過去必須滿足以下任意條件:

• 本身的最長回文字串可以到整個右邊的邊界
• 本身的最長回文字串可以碰到上一條可以的回文中心

這個自己畫圖想想就懂了

代碼↓

#include <bits/stdc++.h>
using namespace std;
const int MN=5e6+516;
string rs; char s[MN];
int d[MN], length=1, can[MN], ans=0;
void Read(){
    s[0]='$', s[length]='-';
    for(auto c:rs){
        s[++length]=c;
        s[++length]='-';
    }
    s[length]='-';
}
void Manacher(){
    for(int i=1,j=0,zhou=0; i<=length; ++i){
        d[i]=min(d[(zhou<<1)-i],j-i+1);
        while(s[i+d[i]]==s[i-d[i]]) d[i]++;
        if(i+d[i]>j){
            j=i+d[i]-1;
            zhou=i;
        }
    }
}
void init(){
    memset(s,0,sizeof(s));
    memset(can,0,sizeof(can)); ans=0;
    memset(d,0,sizeof(d)); length=1;
}
int main(){
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);int T; cin>>T;
    while(T--){
        init(); cin>>rs; Read(); Manacher();
        for(int i=length; i>=1; --i){
            if(s[i]=='-') continue;
			if (i+d[i]-1==length) can[i]=1;
			else if(can[i+d[i]-2]&&i==d[i]) can[i]=1;            
        }
        for(int i=1; i<=length; ++i) if(can[i]) cout<<(i/2)<<" ";
        cout<<'\n';
    }
    return 0;
}

最后一道

CF17E Palisection

給定一個長度為 n 的小寫字母串 S，求有多少對相交的回文子串（包含也算相交）。

注意是多少對

這個咋整? 看到相交, 還有回文子串, 我們會往回文子串上邊去想

我們如果知道了回文半徑, 那么去計算不相交很簡單

那么就把所有的減去不相交的

具體如何去算?

\(f[i]\) 表示以 \(i\) 開頭的回文串有幾個

\(g[i]\) 表示以 \(i\) 結尾的回文串有幾個

\(sum[i]\) 是 \(g[i]\) 的前綴和

一個位置的貢獻是 \(sum[i]*f[i+1]\)

就是前邊所有可以被拎出來的和當前位置的搞一個乘法原理

這樣我們把所有的加起來就行

\(f[i],g[i]\) 我們用 線段樹或者樹狀數組 差分來求.

跑完一次 \(Manacher\) 之后, 我們對于每一個點搞差分, 作如下操作

f[i-d[i]+1]++;
f[i+1]--;
g[i]++; 
g[i+d[i]]--;

很好理解, 一個位置對于 \(f[i]\) 的貢獻是 \([i-d[i]+1,i]\) 的

同理對于 \(g[i]\) 的貢獻是 \([i,i+d[i]-1]\) 的

就這樣搞, 最后一加, 直接統計

代碼↓

#include <bits/stdc++.h>
#define int long long
using namespace std;
const int MN=5e6+516;
const int mod=51123987;
int n, ans, sum, tot, f[MN], g[MN], d[MN];
char s[MN]; string sc;
int length=1;
void Manacher(){
    s[0]='*'; s[length]='-';
    for(auto c:sc){
        s[++length]=c;
        s[++length]='-';
    }
    s[length]='-';
    for(int i=1,j=0,zhou=0; i<=length; ++i){
        d[i]=min(d[(zhou<<1)-i],j-i+1);
        while(s[i+d[i]]==s[i-d[i]]) ++d[i];
        if(i+d[i]>j){
            j=i+d[i]-1;
            zhou=i;
        }
        tot=(tot+(d[i]>>1)%mod)%mod;
    }
}
signed main(){
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0); 
    cin>>n>>sc; Manacher();
    for(int i=1; i<=length; ++i){
        f[i-d[i]+1]++; f[i+1]--;
        g[i]++; g[i+d[i]]--;
    }
    for(int i=1; i<=length; ++i){
        f[i]+=f[i-1]; g[i]+=g[i-1];
    }
    ans=tot*(tot-1)/2%mod;
    for(int i=2; i<=length-2; i+=2){
        sum=(sum+g[i])%mod;
        ans=(ans-sum*f[i+2]%mod+mod)%mod;
    }
    cout<<ans<<'\n';
    return 0;
}
/*
- 1
b 2
- 1
a 4
- 1
b 2
- 3
b 2
- 1
*/

就這樣, 喵