###分類

Transaction  交易

Fraudulent 欺詐

0 is the negative class   ：0是負拷貝類

 

分類  0 、 1

通常用1表示我們需要找的，0表示沒有

 

假設函數

Threshold 閾值

Horizontal  橫軸

在分類上y是0或1 ，但在線性回歸問題上y可能遠大于1遠小于0，所以logistic regression出來了，它就是叫做logistic回歸（實際上就是一種分類算法）的算法。

 

#####假設陳訴

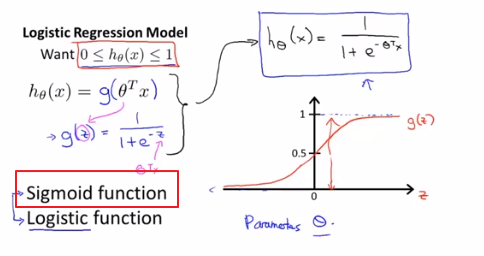
Logistic函數（sigmoid function=logistics function 指代某個函數）

Given this hypothesis representation,what we need to do ,as before ,is fit the parameters theta to our data.

有了假設函數后，我們要做的和之前一樣，就是用參數θ擬合我們的數據。

Hypothesis will then let us make predictions .

假設函數會幫我們作出預測

#####決策界限

Decision boundary 決策邊界

G of z  代表的是g(z)

 

We will predict Y equals 1,whenever theta  transpose axis greater than or equal to 0.And we will predict Y is equal to zero whenever theta transpose X is less than zero.

當θ^TX大于等于0時預測Y為1，當它小于0時就預測Y為0.

So long as we’ve given my parameter vector θ,that defines the decision boundary which is the circle.

只要給定了參數向量θ，圓形的決定邊界就確定了。

But the training set is not what we use to define decision boundary .The training set may be used to fit the parameters θ.Once you have the parameters θ，that is what defines the decision boundary.

我們不是用訓練集來定義的決策邊界，我們訓練集來你和參數θ。但是一旦你有了參數θ，它就確定了決策邊界。

 

This line there is called the dicision boundary.

我們把這條線叫做決策邊界

Actually,this line corresponds to this set of points.

這條決策邊界實際上對應一系列的點（θ^TX）。

Visualization 可視化

 

This decision boundary and a region where we predict 1 equals versus Y equals 0.That’s a property of the hypothesis and of the parameters of the hypothesis，and not a property of the data set.

這條決策邊界和我們預測y=1和y=0的區域。他們都是假設函數的屬性，取決于其參數，他不是數據集的屬性。

 

By adding these more complex polynomial terms to my features as well,I can get more complex decision boundaries that don’t just try to separate the positive and negative examples with a straight line.

通過在特征中增加這些復雜的多項式，我可以得到更復雜的決定邊界，而不只是用直線分開正負樣本。

 

###代價函數

How to fit the parameters theta

如何你和logistic回歸

 

Squared error term 平方誤差項

 

The cost function is 1/m times the sum over my training set of this cost term here.

代價函數是cost項在訓練集范圍的求和

 

If we could minimize this cost function that is plugged into J here,that will work okey.But if we use this particular cost function ，this would be a non-convex function of the parameters theta.

如果我們可以最小化函數J里面的這個代價函數，它也能工作。但是如果我們使用這個代價函數，他會變成參數θ的非凸函數。

 

 

For logistic regression ,this function H here has a non linearity.J of θ may have many local optima 。

對于logistic回歸來說，H函數是非線性的（因為是θ^TX相關的函數）。J(θ)可能有許多的局部最優解----這就是一個非凸函數。

If you were to run gradient descent on this sort of function,it is not guaranteed to converge to the global mininum.

如果你把梯度下降法用在一個這樣的函數（指的就是上面的非凸函數）,不能保證它會收斂到全局最小值。

所以我們希望我們的代價函數J(θ)是一個凸函數，a single bow-shaped function一個單弓形函數，如果是一個純純的凸函數，使用梯度下降法就能保證會收斂到全局最小值。

 

讓J(θ)代價函數變為非凸函數的原因是我們使用sigmod函數來定義H，里面有平方項。So what we would like to do

Is instead come up with a different function that is convex and so that we can apply a great algorithm like gradient descent and be guaranteed to find a global minimum.【所以我們要用別的凸函數，以便我們可以更好的使用像梯度下降的算法并且得到全局最小值】

 

penalty 懲罰

Blow up 激增

Infinite 無限

 

###簡化代價函數和梯度下降函數

Compress ... into  ... 壓縮、合并

Derive  推導

 

Bring the minus sign outside 把負號放在外面

Maximum likelihood estimation  極大似然值

 

The way we’re going to minimize the cost function is using gradient descent.

最小化代價函數的方法是使用梯度下降法。

We repeatedly update each parameter by updating it as itself minus a learning rate alpha this derivative term.

我們要反復更新每個參數，就是用他自己減去學習率α乘以后面的導數項。

假設函數的定義發生了變化，所以和線性回歸的梯度下降是完全不一樣的。

 

Even though the update rule looks cosmetically identical，because the definition of the hypothesis changed,this is actually not the same thing as gradient descent for linear regression.

 

即使更新參數的規則看起來基本相同，但由于假設的定義發生了變化，所以梯度下降和logistic回歸是不一樣的算法。

 

Monitor  監視

 

Converge 收斂

 

 

Features scaling can help gradient descent converge faster for linear regression.

特征縮放可以提高梯度下降的收斂速度。

特征縮放統一適用于logistic回歸。

 

 

###高級優化

Last 上一個、最后

Advanced optimization algorithms 高級優化算法

 

Gradient descent repeat perform the following update.

梯度下降算法做的就是反復執行這些，來更新θ參數。

梯度下降并不是唯一的minimize the cost function【最小化代價函數的】算法，還有別的advanced,sophisticated優化算法。

 

Advanced numerical computing 高等數值

Property 特性

Manually 手動

These algorithms is that given these the way to compute the derive and a cost function,we can think of these algorithms as a clever inner-loop called a kine search algorithm .

這些算法的一種思路是，給出計算導數項和代價函數的方法。想象這些算法有一個叫做線搜索算法的智能內循環，

 

 

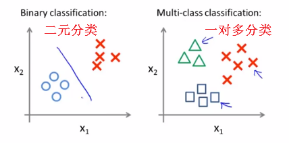
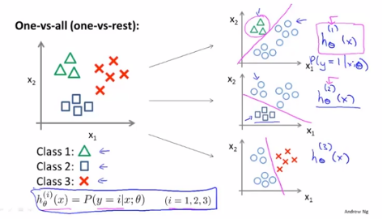
###多元分類：一對多

One-versus-all 一對多

Y can take on a small number of discrete values

Y可以取一些離散值

Positive  ，negative