做編譯原理作業是遇到的一類比較繁瑣的題，記錄一下。??

大體流程

• 由正規式得出NFA的狀態轉換圖
• 根據NFA的狀態轉換圖寫出NFA確定化為DFA的狀態轉換矩陣
• 根據上述矩陣中的重命名寫出DFA重新命名狀態轉換矩陣表
• 化簡所得到的DFA
• 畫出DFA的狀態轉換圖

正規式->NFA的狀態轉換圖

要領比較簡單，有點像連電路圖，注意一下初態和終態的畫法，以下是其他注意事項。

• ‘·’：一般會省去，由于連接前后各個字符串，畫的時候當成串聯下一狀態就行
• ‘|’：或，連接時分出分支指向各自下一狀態，像是并聯
• ‘()’：優先計算，可以先單獨處理成一個小單元，畫好后再連頭尾
• 上標‘*’：閉包，連向狀態自己
• 上標‘+’：正閉包，我目前還沒見過，個人感覺是比起上標‘*’前多加一個串聯的狀態

NFA的狀態轉換圖->NFA確定化為DFA的狀態轉換矩陣

有點繁瑣，是一個一遍遍掃描的過程。??

1. 第一行寫上各列名稱，分別為：重新命名、輸入狀態、n個輸入字符
2. 將初態名填入下一行的輸入狀態
3. 觀察圖上在初態位置上，輸入某個輸入字符x后下一步可以轉向哪些狀態，并將它們依次寫在表格（初態，x）中，若無狀態可轉移則不填，注意，轉移向自己也要填上，狀態間用“,”隔開
4. 重復3的操作直到該行所有輸入字符都已嘗試
5. 觀察本行填寫的結果，將每個單元格的結果都視作一個狀態集合，若為空則無視，將所有新出現過的狀態集合（注：不同順序但同元素視為同一個狀態集合）依次填入輸入狀態中的各格
6. 仿照3、4的操作，記錄各輸入狀態后續出現的狀態集合，
7. 當沒有新的輸入狀態出現，也就是無新增可填時則結束
8. 此時重新命名那一列還未填寫，可根據自己的喜好為其填入字符名稱，如A、B、C或1、2、3等，為了后續方便，建議盡可能簡潔有序
   至此矩陣的構建結束

寫出DFA重新命名狀態轉換矩陣表

這一步很簡單哦。??

簡要地來說，就是將上一步得到的矩陣去掉重命名那一列，將各輸入狀態的重命名回代到矩陣中去，全部其換掉，這一步就完成了！

化簡所得到的DFA

這一步簡要地將就是將各狀態重新劃分為塊，但是有點繞。??

1. 首先將上一步得到的各輸入狀態劃分為兩個集合，一個叫非終態組，一個叫終態組。顧名思義，后者中的所有輸入狀態均包含終態；前者的則均不包含終態。
2. 對于每個集合，我們進行這樣的討論：
   2.1. 選擇輸入字符x進行輸入，觀察集合中各輸入狀態在輸入x后轉移的輸入狀態A1（即DFA矩陣中的（輸入狀態，x））、A2、A3...。
   2.2. 若轉移的輸入狀態均屬于現在劃分的同一集合，則無事發生；若不屬于現在劃分的同一集合，則計劃在本輪操作后，將轉移后不屬于當前劃分同一集合的都分開為新的集合。
3. 對每個集合討論完后，我們將討論中要分開的集合拆開，得到新的一組集合劃分。
4. 對得到的新的一組集合劃分，重復2、3的操作，直至無法再分，得不出新的集合劃分。
5. 操作4結束后的一組集合劃分中，若存在包含多個元素的集合，則將其替換為僅包含其中一個元素的集合（即單元素集合），得到新的一組集合劃分，該結果即為化簡結果。
6. 重寫化簡后的矩陣，對于上一過程得到的矩陣，替換元素覆寫其替換集合的所有元素，出現重復的便刪除，化簡完成！

畫出DFA的狀態轉換圖

勝利在望啊，同志們！??

根據化簡后的矩陣畫出狀態轉移圖，過于簡單，不再贅述。

題目舉例

以下是我自己作業的一次內容，供參考，如有錯誤請一定不吝指正！

題目描述

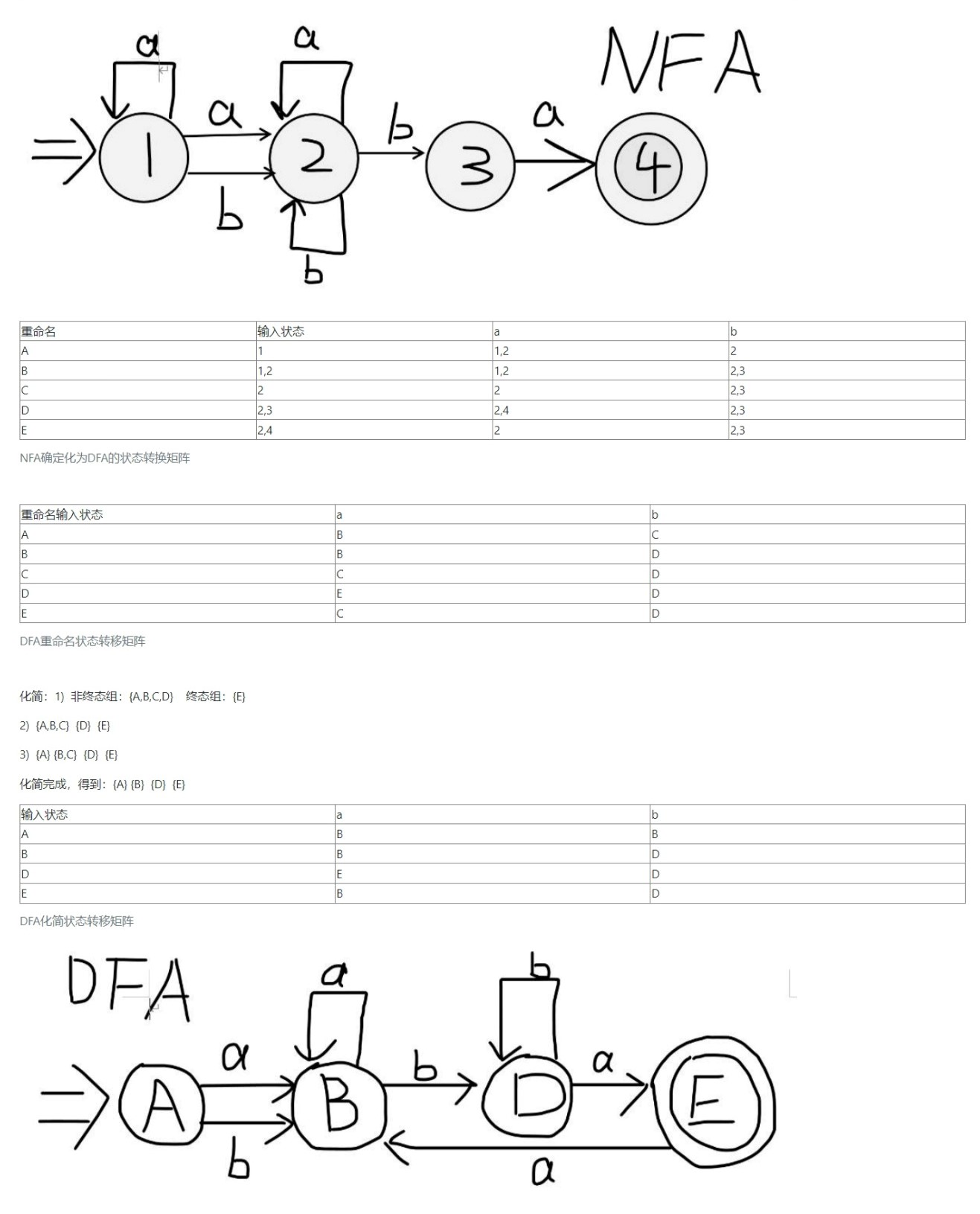
構造與正規式a（b|a)(a|b)ba等價的NFA，然后對NFA確定化為DFA，最后對DFA化簡。要求NFA和DFA以圖形方式描述。

解題示例

剛把得！??