2023-2024-1 20231302《計算機基礎與程序設計》第六周學習總結
作業信息
| 這個作業屬于哪個課程 | 2023-2024-1-計算機基礎與程序設計 |
|---|---|
| 這個作業要求在哪里 | 2023-2024-1計算機基礎與程序設計第六周作業 |
| 這個作業的目標 | Polya如何解決問題、簡單類型與組合類型、復合數據結構、查找與排序算法、算法復雜度、遞歸、代碼安全 |
| 作業正文 | http://www.rzrgm.cn/9q2z2z/p/17809813.html |
教材學習內容總結
《計算機科學概論》
- 本章先由poyla算法開始,告訴我們如何用計算機解決問題,解決問題應該以哪些步驟去進行。用偽代碼介紹了介紹了一些算法,其中包括有簡單參數的算法,復雜變量,搜索算法和排序,遞歸算法。最后介紹了信息隱蔽的概念,這里又一次地體現了抽象這一重要概念的重要性。
《C語言程序設計》
- 本章介紹了算法的概念,并且介紹了它的描述方法,后文著重通過流程圖介紹了不同的算法語句,包括了單、雙、多分支條件語句,并在其中介紹了條件運算符和條件表達式。多路選擇的switch語句和邏輯運算符和邏輯表達式。并且學習了程序測試的有關內容。
教材學習中的問題和解決過程
- 問題1:我在學習搜索算法時,學習到了順序搜索、二分檢索,它們都是基于有序排列的,但是一組數據如果沒有順序,是否就不能用搜索算法了呢,如果能的話,那個算法又是什么形式呢
- AI回答:即使一組數據沒有順序,仍然可以使用搜索算法來查找特定元素。在無序數據中進行搜索的一種常見算法是線性搜索(Linear Search),也稱為順序搜索(Sequential Search)。
線性搜索算法從數據的開頭開始逐個比較元素,直到找到目標元素或搜索完整個數據集。它的時間復雜度是O(n),其中n是數據的大小。
雖然線性搜索在無序數據中的效率較低,但對于小型數據集或者不需要頻繁搜索的情況,它仍然是一種簡單有效的搜索算法。
以下是一個示例的線性搜索算法的偽代碼:
function linearSearch(array, target):
for i from 0 to length of array - 1:
if array[i] equals target:
return i
return -1
在這個偽代碼中,我們遍歷數組中的每個元素,如果找到目標元素,則返回其索引。如果遍歷完整個數組仍未找到目標元素,則返回-1。
需要注意的是,線性搜索算法的效率取決于數據的大小,因此在大型數據集中,使用基于有序數據的搜索算法(如二分搜索)可能更加高效。但是對于無序數據,線性搜索仍然是一種可行的搜索算法。
- 問題2:書中提到遞歸法有程序運行效率低的缺點,并且講到若提高程序運行效率,宜以迭代形式替代遞歸形式。我在這里想要了解一下迭代形式是什么樣子的,通過一些例子了解一下它是怎樣運行的。
- AI 回答
迭代形式是一種通過循環結構來實現算法邏輯的方法,相對于遞歸形式,它更加高效。在迭代中,算法通過迭代變量的更新和條件判斷來控制循環的執行,直到達到預期的結果。
舉個例子,我們可以通過迭代來實現計算一個數的階乘。下面是使用迭代形式計算階乘的示例代碼:
int factorial(int n) {
int result = 1;
for (int i = 1; i <= n; i++) {
result *= i;
}
return result;
}
int main() {
int n = 5;
int result = factorial(n);
printf("The factorial of %d is %d\n", n, result);
return 0;
}
在這個例子中,我們使用了for循環來進行迭代計算階乘。循環變量i從1逐步增加到n,每次循環將當前的i乘以result,并將結果存回result中。最終,當循環結束時,result中保存的就是n的階乘值。
通過迭代,我們避免了遞歸中不斷調用函數的開銷,提高了程序的運行效率。迭代形式在C語言中是常見且重要的編程技術,可用于解決各種循環和迭代計算問題。
在第六行代碼 result = i 中,= 是一個復合賦值運算符,用于將 result 乘以 i 的值,并將結果再次賦給 result。這行代碼的作用是將當前的迭代變量 i 乘以 result 的值,然后將結果存回 result 中。
更詳細地解釋,result *= i 可以理解為 result = result * i。在每次循環中,result 的值都會與當前的迭代變量 i 相乘,并將乘積結果存回 result 中。這樣隨著循環的進行,result 逐漸累積乘積的值,最終得到 n 的階乘。
例如,在計算階乘 n 為 5 的情況下,初始時 result 的值為 1。在第一次循環中,i 的值為 1,所以執行 result *= i 后,result 的值變為 1。接著,在第二次循環中,i 的值為 2,所以執行 result *= i 后,result 的值變為 2。依此類推,直到循環結束,result 的值將變為 n 的階乘,即 120。
這行代碼的目的是不斷更新 result 的值,使其保存當前迭代的乘積結果,從而最終得到整個階乘的結果。
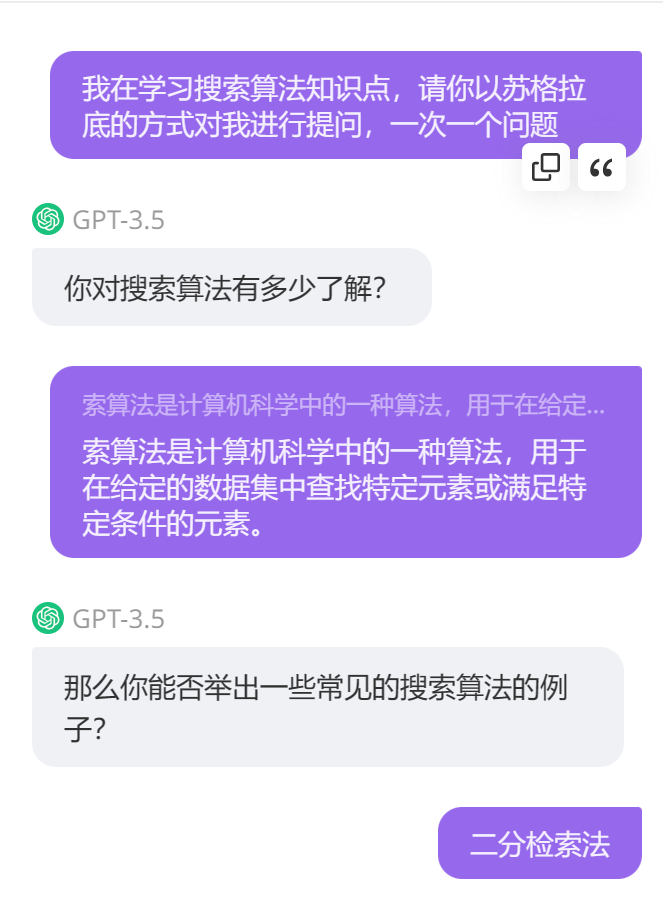
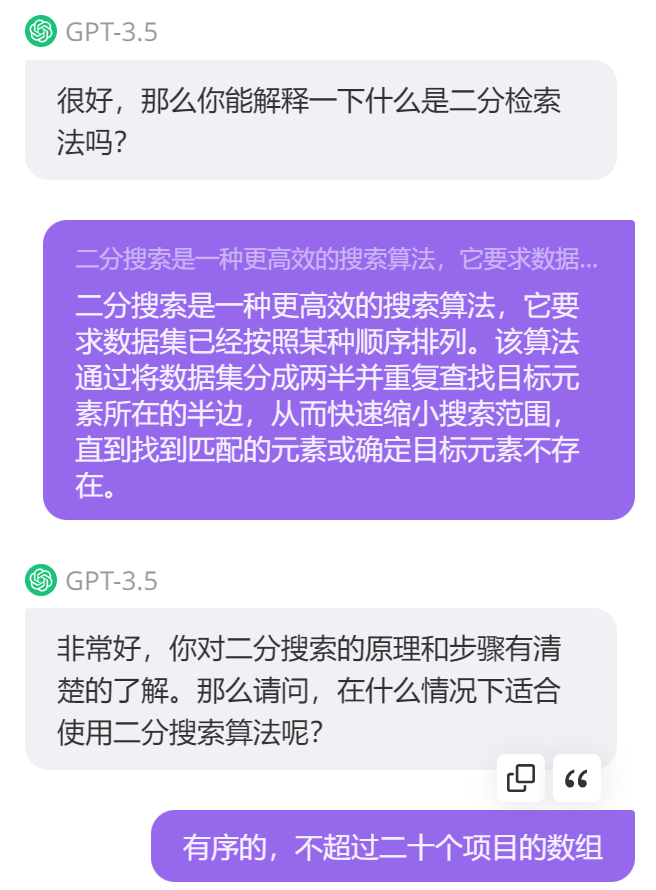
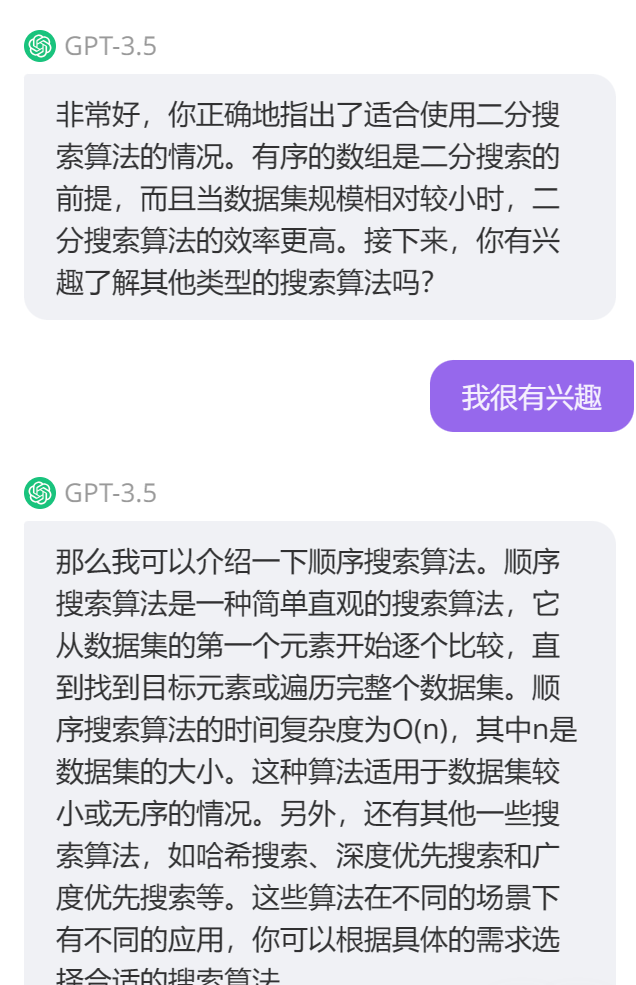
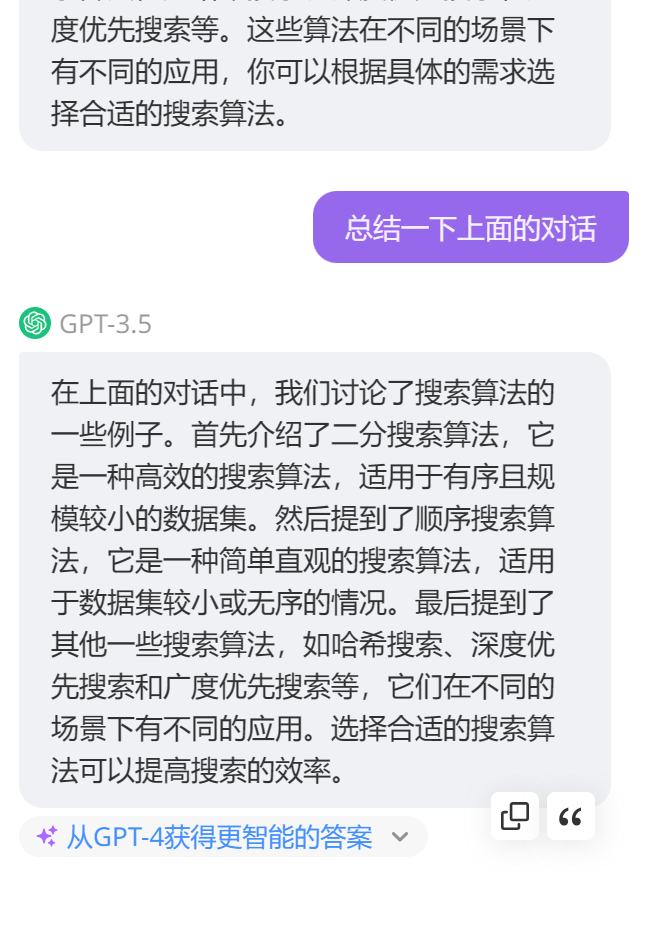
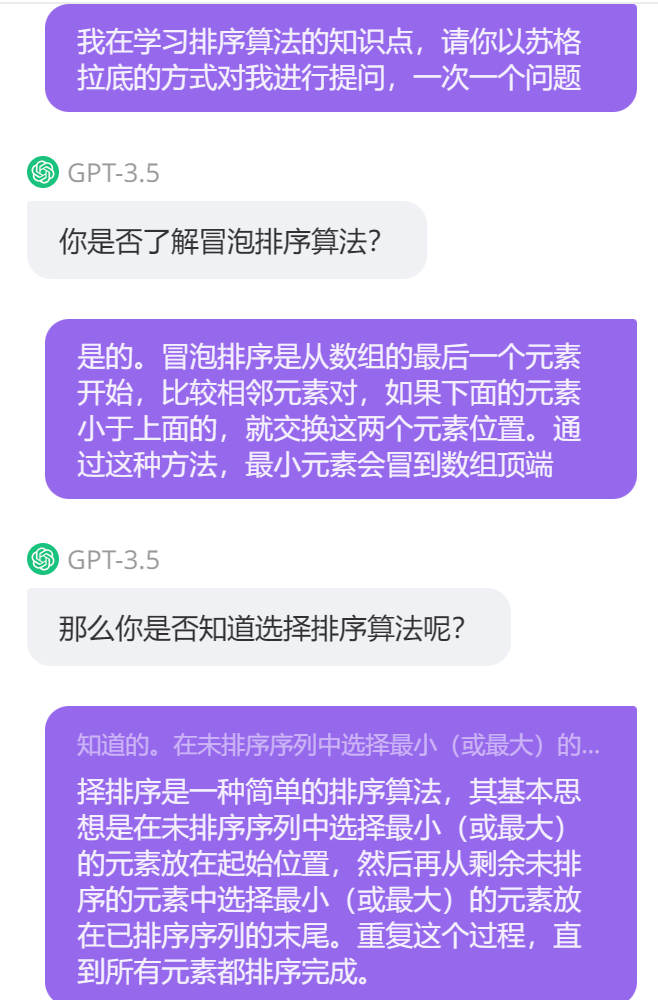
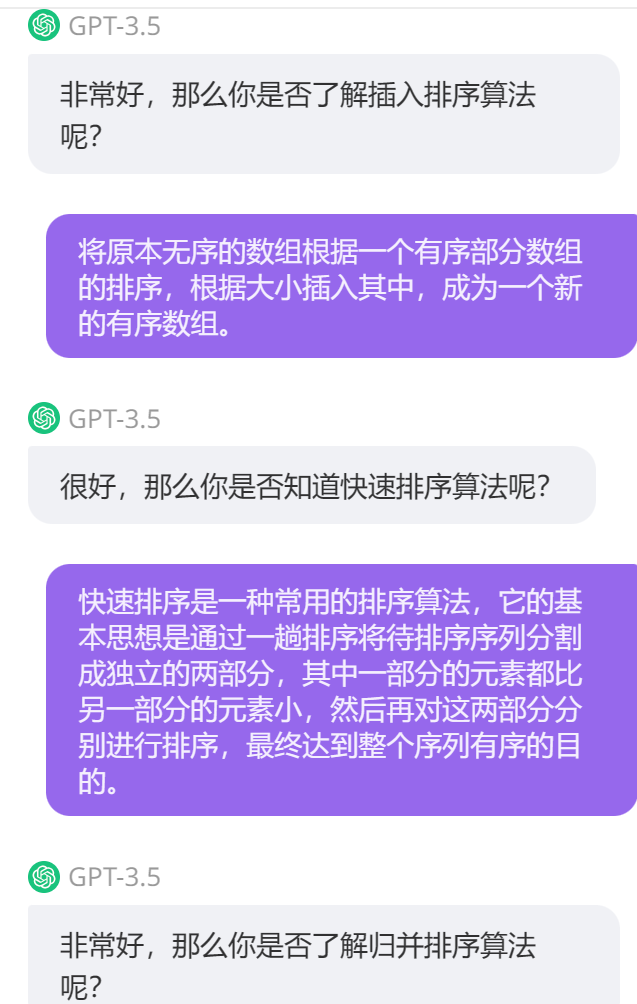
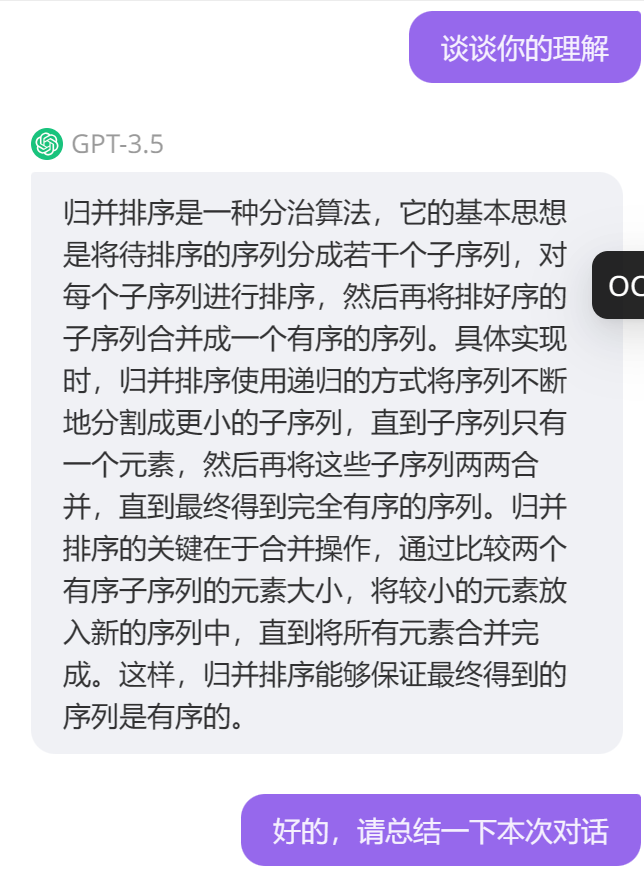
基于AI的學習



 浙公網安備 33010602011771號
浙公網安備 33010602011771號