基于PSO粒子群優(yōu)化算法的64QAM星座圖的最優(yōu)概率整形matlab仿真,對(duì)比PSO優(yōu)化前后整形星座圖和誤碼率
1.算法仿真效果
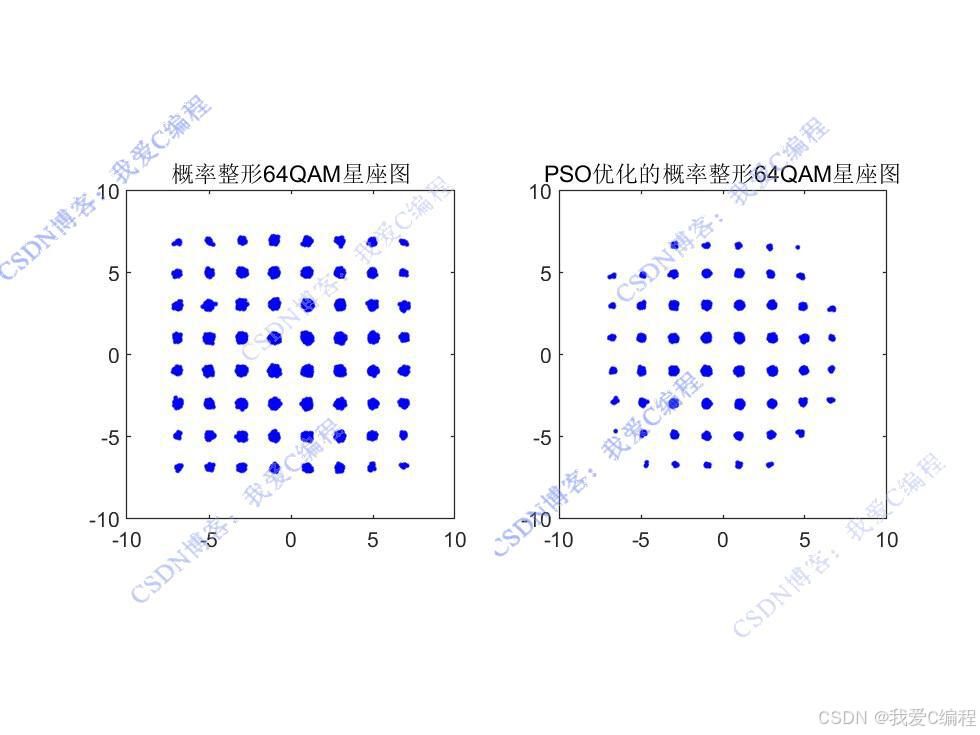
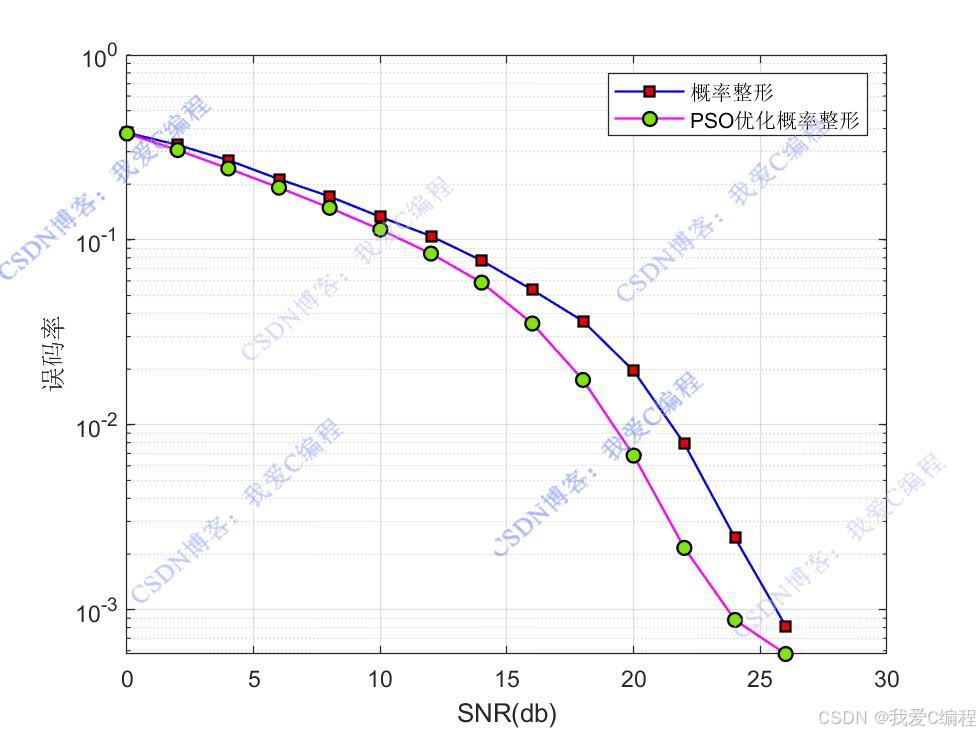
仿真操作步驟可參考程序配套的操作視頻。
2.算法涉及理論知識(shí)概要
64QAM是一種高階調(diào)制方式，星座圖中有64個(gè)星座點(diǎn)，每個(gè)星座點(diǎn)對(duì)應(yīng)6比特信息。傳統(tǒng)的74QAM采用均勻分布。通過改變改變星座圖不同位置符號(hào)出現(xiàn)的概率，讓外圈星座點(diǎn)出現(xiàn)頻率降低，有利于減小平均功率，相當(dāng)于增加了最小歐氏距離，從而有更好的傳輸性能。這就是我們所說的概率星座整形（PCS）了。它究竟有什么好處呢？
1. 具有整形增益。
2. 有望達(dá)到更高的傳輸容量，顯著提升頻譜效率。
3. 傳輸速率可以靈活調(diào)整，以完美適配不同的傳輸信道。
4. 無須多種支持多種QAM映射，僅使用方形QAM調(diào)制，需調(diào)整整形系數(shù)
PCS的關(guān)鍵在于如何對(duì)均勻概率的輸出映射成非均勻概率幅度分布，而且該概率分布還應(yīng)該是最優(yōu)的。理論上可以證明Maxwell-Boltzman分布對(duì)于方形QAM整形是最優(yōu)的概率分布。概率星座整形一般使用如下的公式完成：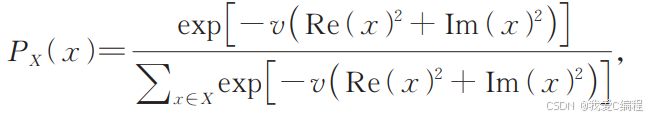
參數(shù)v為整形因子。在本課題中，將通過PSO優(yōu)化算法，搜索最佳的參數(shù)v，進(jìn)一步提升概率整形后的系統(tǒng)性能。以64QAM 的誤碼率（BER）作為適應(yīng)度函數(shù)。誤碼率越低，表明該概率整形因子 對(duì)應(yīng)的星座點(diǎn)概率分布越優(yōu)。在實(shí)際計(jì)算時(shí)，可通過蒙特卡羅仿真來估計(jì)誤碼率。具體步驟為：依據(jù)當(dāng)前的 計(jì)算每個(gè)星座點(diǎn)的發(fā)送概率，生成大量發(fā)送符號(hào)，經(jīng)過加性高斯白噪聲（AWGN）信道傳輸，接收符號(hào)并進(jìn)行解調(diào)，統(tǒng)計(jì)錯(cuò)誤比特?cái)?shù)，進(jìn)而計(jì)算誤碼率。
通過PSO算法，獲得最優(yōu)的參數(shù)v，以降低64QAM 的誤碼率。
3.MATLAB核心程序
......................................................................
for i=1:Iter
i
for j=1:Npeop
rng(i+j)
if func_obj(x1(j,:))<pbest1(j)
p1(j,:) = x1(j,:);%變量
pbest1(j) = func_obj(x1(j,:));
end
if pbest1(j)<gbest1
g1 = p1(j,:);%變量
gbest1 = pbest1(j);
end
v1(j,:) = 0.8*v1(j,:)+c1*rand*(p1(j,:)-x1(j,:))+c2*rand*(g1-x1(j,:));
x1(j,:) = x1(j,:)+v1(j,:);
for k=1:dims
if x1(j,k) >= tmps(2,k)
x1(j,k) = tmps(2,k);
end
if x1(j,k) <= tmps(1,k)
x1(j,k) = tmps(1,k);
end
end
for k=1:dims
if v1(j,k) >= tmps(2,k)/2
v1(j,k) = tmps(2,k)/2;
end
if v1(j,k) <= tmps(1,k)/2
v1(j,k) = tmps(1,k)/2;
end
end
end
gb1(i)=gbest1
end
figure;
plot(gb1,'-bs',...
'LineWidth',1,...
'MarkerSize',6,...
'MarkerEdgeColor','k',...
'MarkerFaceColor',[0.9,0.0,0.0]);
xlabel('優(yōu)化迭代次數(shù)');
ylabel('適應(yīng)度值');
VV = g1;
save PSO_OPT.mat gb1 VV
0X_079m
4.完整算法代碼文件獲得
V
浙公網(wǎng)安備 33010602011771號(hào)