01背包問題描述

已知:有一個容量為V的背包和N件物品，第i件物品的重量是weight[i]，收益是cost[i]。

限制:每種物品只有一件，可以選擇放或者不放

問題:在不超過背包容量的情況下，最多能獲得多少價值或收益

相似問題:在恰好裝滿背包的情況下，最多能獲得多少價值或收益

這里，我們先討論在不超過背包容量的情況下，最多能獲得多少價值或收益。

基本思路

01背包的特點:每種物品只有一件，可以選擇放或者不放

子問題定義狀態

f[i][v] : 前i件物品放到一個容量為v的背包中可以獲得最大價值

狀態轉移方程

f[i][v] = max(f[i - 1][v],f[i - 1][v - weight[i]] + cost[i])

分析

考慮我們的子問題，將前i件物品放到容量為v的背包中，若我們只考慮第i件物品時，它有兩種選擇，放或者不放。

1) 如果第i件物品不放入背包中，那么問題就轉換為：將前i - 1件物品放到容量為v的背包中，帶來的收益f[i - 1][v]

2) 如果第i件物品能放入背包中，那么問題就轉換為：將前i - 1件物品放到容量為v - weight[i]的背包中，帶來的收益f[i - 1][v - weight[i]] + cost[i]

代碼

#include <iostream>
using namespace std;

const int N = 3;//物品個數
const int V = 5;//背包最大容量
int weight[N + 1] = {0,3,2,2};//物品重量
int value[N + 1] = {0,5,10,20};//物品價值

int f[N + 1][V + 1] = {{0}};

int Max(int x,int y)
{
	return x > y ? x : y;
}

/*
目標：在不超過背包容量的情況下，最多能獲得多少價值

子問題狀態:f[i][j]:表示前i件物品放入容量為j的背包得到的最大價值

狀態轉移方程:f[i][j] = max{f[i - 1][j],f[i - 1][j - weight[i]] + value[i]}

初始化:f數組全設置為0
*/
int Knapsack()
{
	//初始化
	memset(f,0,sizeof(f));
	//遞推
	for (int i = 1;i <= N;i++) //枚舉物品
	{
		for (int j = 0;j <= V;j++) //枚舉背包容量
		{
			f[i][j] = f[i - 1][j];
			if (j >= weight[i])
			{
				f[i][j] = Max(f[i - 1][j],f[i - 1][j - weight[i]] + value[i]);
			}
		}
	}
	return f[N][V];
}

int main()
{
	cout<<Knapsack()<<endl;
	system("pause");
	return 1;
}

效率分析：

此算法的時間復雜度為O(N*V)，空間復雜度也為O(N*V)。其中，N 表示物品個數，V 表示背包容量這里，時間復雜度不可以在優化了，但是空間復雜度可以繼續優化到O(V)

優化空間復雜度

上述的方法，我們使用二維數組 f[i][v] 保存中間狀態，這里我們可以使用一維數組f[v]保存中間狀態就能得到結果

分析

我們現在使用f[v]保存中間狀態，我們想要達到的效果是，第i次循環后，f[v]中存儲的是前i個物體放到容量v時的最大價值

在回顧下之前講過的狀態轉移方程：

f[i][v] = max(f[i - 1][v],f[i - 1][v - weight[i]] + cost[i])

我們可以看到，要想得到 f[i][v]，我們需要知道 f[i - 1][v] 和 f[i - 1][v - weight[i]]，由于我們使用二維數組保存中間狀態，所以可以直接取出這兩個狀態。

當我們使用一維數組存儲狀態時，f[v]表示，在執行i次循環后(此時已經處理i個物品)，前i個物體放到容量v時的最大價值，即之前的f[i][v]。與二維相比較，它把第一維隱去了，但是二者表達的含義還是相同的，只不過針對不同的i，f[v]一直在重復使用，所以，也會出現第i次循環可能會覆蓋第i - 1次循環的結果。

為了求f[v],我們需要知道，前i - 1個物品放到容量v的背包中帶來的收益，即之前的f[i - 1][v]  和 前i - 1件物品放到容量為v - weight[i]的背包中帶來的收益，即之前的f[i - 1][v - weight[i]] + cost[i]。

難點：由于我們只使用一維數組存儲，則在求這兩個子問題時就沒有直接取出那么方便了，因為，第i次循環可能會覆蓋第i - 1次循環的結果。

現在我們來求這兩個值

1）前i - 1個物品放到容量v的背包中帶來的收益，即之前的f[i - 1][v] ：

由于，在執行在i次循環時，f[v]存儲的是前i個物體放到容量v時的最大價值，在求前i個物體放到容量v時的最大價值(即之前的f[i][v])時，我們是正在執行第 i 次循環，f[ v ]的值還是在第 i - 1  次循環時存下的值，在此時取出的 f[ v ]就是前i - 1個物體放到容量v時的最大價值，即f[i - 1][v]。

2）前i - 1件物品放到容量為v - weight[i]的背包中帶來的收益，即之前的f[i - 1][v - weight[i]] + cost[i]

由于，在執行第i次循環前，f[0 ~ V]中保存的是第i - 1次循環的結果，即是前i - 1個物體分別放到容量0 ~ V時的最大價值，即f[i - 1][0 ~ V]。

則，在執行第i次循環前，f 數組中v - weight[i]的位置存儲就是我們要找的 前i - 1件物品放到容量為v - weight[i]的背包中帶來的收益 (即之前的f[i - 1][v - weight[i]])，這里假設物品是從數組下標1開始存儲的。

偽代碼

for i=1..N //枚舉物品
    for v=V..0 //枚舉容量，從大到小
        f[v]=max{f[v],f[v-weight[i]] + cost[i]};

由上面偽代碼可知，在執行第 i 次循環時，需要把背包容量由V..0都要遍歷一遍，檢測第 i 件物品是否能放。

逆序枚舉容量的原因：

注意一點，我們是由第 i - 1 次循環的兩個狀態推出 第 i 個狀態的，而且 v  > v - weight[i]，則對于第i次循環，背包容量只有當V..0循環時，才會先處理背包容量為v的狀況，后處理背包容量為 v-weight[i] 的情況。

具體來說，由于，在執行v時，還沒執行到v - weight[i]的，因此，f[v - weight[i]]保存的還是第i - 1次循環的結果。即在執行第i次循環 且 背包容量為v時，此時的f[v]存儲的是 f[i - 1][v] ，此時f[v-weight[i]]存儲的是f[i - 1][v-weight[i]]。

相反，如果在執行第 i 次循環時，背包容量按照0..V的順序遍歷一遍，來檢測第 i 件物品是否能放。此時在執行第i次循環 且 背包容量為v時，此時的f[v]存儲的是 f[i - 1][v] ，但是，此時f[v-weight[i]]存儲的是f[i][v-weight[i]]。

因為，v  > v - weight[i]，第i次循環中，執行背包容量為v時，容量為v - weight[i]的背包已經計算過，即f[v - weight[i]]中存儲的是f[i][v - weight[i]]。即，對于01背包，按照增序枚舉背包容量是不對的。

代碼

#include <iostream>
using namespace std;

const int N = 3;//物品個數
const int V = 5;//背包最大容量
int weight[N + 1] = {0,3,2,2};//物品重量
int value[N + 1] = {0,5,10,20};//物品價值

int f[V + 1] = {0};

int Max(int x,int y)
{
	return x > y ? x : y;
}

/*
目標：在不超過背包容量的情況下，最多能獲得多少價值

子問題狀態:f[j]:表示前i件物品放入容量為j的背包得到的最大價值

狀態轉移方程:f[j] = max{f[j],f[j - weight[i]] + value[i]}

初始化:f數組全設置為0
*/
int Knapsack()
{
	//初始化
	memset(f,0,sizeof(f));
	//遞推
	for (int i = 1;i <= N;i++) //枚舉物品
	{
		for (int j = V;j >= weight[i];j--) //枚舉背包容量,防越界，j下限為 weight[i]
		{
			f[j] = Max(f[j],f[j - weight[i]] + value[i]);
		}
	}
	return f[V];
}

int main()
{
	cout<<Knapsack()<<endl;
	system("pause");
	return 1;
}

但是，增序枚舉背包容量會達到什么效果：它會重復的裝入某個物品，而且盡可能多的，使價值最大，當然不會不超過背包容量

而逆序枚舉背包容量：背包中的物品至多裝一次，使價值最大，當然不會不超過背包容量

我們首先舉例說明：

逆序枚舉物品

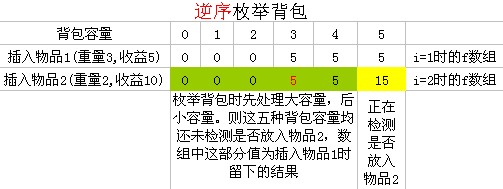
當i = 2，我們要求 f [5]：表示檢測物品2放入容量為5的背包的最大收益

上圖表示，當i = 2，求f[5]時f數組的狀況，

橙色為數組現在存儲的值，這些值是i = 1時(上一次循環)存入數組 f 的。相當于f[i - 1][v]

而黃色使我們要求的值，在求f[5]之前，f[5]= 5，即f[i - 1][5] = 5

現在要求 i = 2 時的f[5] = f[5 - 2] + 10 = 5 + 10 = 15  >  f[i - 1][5] = 5

故，f[5] = 15；

注意一點，在求f[v]時，它引用的 f[v - weight[i]] 和 f[v]都是上一次循環的結果

順序枚舉物品

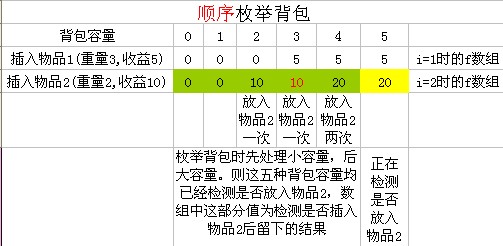
當i = 2，我們要求 f [5]：表示檢測物品2放入容量為5的背包的最大收益

上圖表示，當i = 2，求f[5]時f數組的狀況，

橙色為數組現在存儲的值，這些值是i = 2時(本次循環)存入數組 f 的。相當于f[i][v]

這是由于，我們是增序遍歷數組f的，在求f[v]時，v之前的值(0 ~ v - 1)都已經在第i次循環中求出。

而黃色使我們要求的值，在求f[5]之前，f[5]= 5，即f[i - 1][5] = 5

現在要求 i = 2 時的f[5] = f[5 - 2] + 10 =10+ 10 = 20 >  f[i - 1][5] = 5

故，f[5] = 20；

其中引用的f[3]是相當于f[i][3] 而不是正常的f[i - 1][3]

注意一點，在求f[v]時，它引用的 f[v - weight[i]]是本次循環的結果 而f[v]是上一次循環的結果

換個角度說，

在檢測 背包容量為5時，看物品2是否加入

由狀態轉移方程可知，我們f[5]需要引用自己本身和f[3]

由于背包容量為3時，可以裝入物品2，且收益比之前的大，所以放入背包了。

在檢測f[5]時，肯定要加上物品2的收益，而f[5]在引用f[3]時，f[3]時已經加過一次物品2，

因此，在枚舉背包容量時，物品2會加入多次。

進一步說：

我們觀察一維狀態轉移方程：

f[i][v] = max(f[i - 1][v],f[i - 1][v - weight[i]] + cost[i])

首先我們明確三個問題

1) v - weight[i] < v

2) 狀態f[i][v] 是由 f[i - 1][v] 和 f[i - 1][v - weight[i]] 兩個狀態決定

3) 對于物品i，我們在枚舉背包容量時，只要背包容量能裝下物品i 且 收益比原來的大，就會成功放入物品i。

具體來說，枚舉背包容量時，是以遞增的順序的話，由于 v - weight[i] < v,則會先計算 v - weight[i]。在背包容量為v - weight[i]時，一旦裝入了物品i，由于求f[v]需要使用f[i - 1][v - weight[i]]，而若求f[v]時也可以裝入物品i的話，那么在背包容量為v時，容量為v的背包就裝入可兩次物品。又若v - weight[i]是由之前的狀態推出，它們也成功裝入物品i的話，那么容量為v的背包就裝入了多次物品i了。

注意，此時，在計算f[v]時，已經把物品i能裝入的全裝入容量為v的背包了，此時裝入物品i的次數為最大啊

其實，順序枚舉容量是完全背包問題最簡捷的解決方案。

 

初始化的細節問題

求最優解的背包問題時，有兩種問法：

1)在不超過背包容量的情況下，最多能獲得多少價值

2)在恰好裝滿背包的情況下，最多能獲得多少價值

主要的區別為是否要求恰好裝滿背包。但這兩種問法的實現方法是在初始化的時候有所不同。

1)恰好裝滿背包的情況：使用二維數組f[i][v]存儲中間狀態，其中第一維表示物品，第二維表示背包容量

初始化時，除了f[i][0] = 0（第一列）外，其他全為負無窮。

原因：初始化 f 數組就是表示：在沒有任何物品可以放入背包時的合法狀態。對于恰好裝滿背包，只有背包容量為 0（第一列），可以什么物品都不裝就能裝滿，這種情況是合法情況，此時價值為0。其他f[0][v]（第一列）是都不能裝滿的，此時有容量沒物品。而其他位置（除去第一行和第一列的位置），我們為了在計算中比較最大值，也要初始化為負無窮。我們從程序的角度上看，我們只允許裝入背包物品的序列的起始位置是從第一列開始，這些起始位置都是合法位置，且能恰好裝滿的情況收益均為正值，到f[N][V]終止。

注意，我們雖然是求恰好裝滿，還是需要枚舉所有可以裝入背包的物品，只要能裝入，還需裝入，收益有增加。只不過，由于恰好裝滿的物品的序列肯定是從第一列某行開始的，且之后的收益肯定是正值。對于非恰好裝滿的物品序列，其實位置肯定是從第一行某位置開始的，由于此時被初始化為負無窮，在和那些恰好裝滿物品序列帶來的價值時，肯定是小的。所以，我們最后能獲得最大值。

代碼：

#include <iostream>
using namespace std;

const int MinNum = 0x80000000;

const int N = 3;//物品個數
const int V = 5;//背包最大容量
int weight[N + 1] = {0,3,2,2};//物品重量
int value[N + 1] = {0,5,10,20};//物品價值

int f[N + 1][V + 1] = {{0}};

int Max(int x,int y)
{
	return x > y ? x : y;
}

/*
目標：在恰好裝滿背包的情況下，最多能獲得多少價值

子問題狀態:f[i][j]:表示前i件物品放入容量為j的背包得到的最大價值

狀態轉移方程:f[i][j] = max{f[i - 1][j],f[i - 1][j - weight[i]] + value[i]}

初始化:f數組全設置為0
*/
int Knapsack()
{
	//初始化
	for (int i = 0;i <= N;i++) //枚舉物品
	{
		for (int j = 0;j <= V;j++) //枚舉背包容量
		{
			f[i][j] = MinNum;
		}
	}
	for (int i = 0;i <= N;i++)
	{
		f[i][0] = 0;//背包容量為0時為合法狀態
	}
	//遞推
	for (int i = 1;i <= N;i++) //枚舉物品
	{
		for (int j = 1;j <= V;j++) //枚舉背包容量
		{
			f[i][j] = f[i - 1][j];
			if (j >= weight[i])
			{
				f[i][j] = Max(f[i - 1][j],f[i - 1][j - weight[i]] + value[i]);
			}
		}
	}
	return f[N][V];
}

int main()
{
	cout<<Knapsack()<<endl;//輸出25
	system("pause");
	return 1;
}

使用一維數組f[v]存儲中間狀態，維表示背包容量

初始化時，除了f[0] = 0，其他全為負無窮。

原因：只有容量為0 的背包可以什么物品都不裝就能裝滿，此時價值為0。其它容量的背包均沒有合法的解，屬于未定義的狀態，應該被賦值為負無窮了

代碼

#include <iostream>
using namespace std;

const int MinNum = 0x80000000;//int最小的數

const int N = 3;//物品個數
const int V = 5;//背包最大容量
int weight[N + 1] = {0,3,2,2};//物品重量
int value[N + 1] = {0,5,10,20};//物品價值

int f[V + 1] = {0};

int Max(int x,int y)
{
	return x > y ? x : y;
}

/*
目標：在恰好裝滿背包容量的情況下，最多能獲得多少價值

子問題狀態:f[j]:表示前i件物品放入容量為j的背包得到的最大價值

狀態轉移方程:f[j] = max{f[j],f[j - weight[i]] + value[i]}

初始化:f數組全設置為0
*/
int Knapsack()
{
	//初始化
	for (int i = 0;i <= V;i++)
	{
		f[i] = MinNum;
	}
	f[0] = 0;//只有背包容量為0時才是合法狀態，由合法狀態組成的結果才是合法的

	//遞推
	for (int i = 1;i <= N;i++) //枚舉物品
	{
		for (int j = V;j >= weight[i];j--) //枚舉背包容量,防越界，j下限為 weight[i]
		{
			f[j] = Max(f[j],f[j - weight[i]] + value[i]);
		}
	}
	return f[V];
}

int main()
{
	cout<<Knapsack()<<endl;//輸出25
	system("pause");
	return 1;
}

2)不需要把背包裝滿，只需要收益最大

使用二維數組f[i][v]存儲中間狀態，其中第一維表示物品，第二維表示背包容量

初始化時，除了f[i][0] = 0（第一列）外，其他全為負無窮。

使用一維數組f[v]存儲中間狀態，維表示背包容量

原因：如果背包并非必須被裝滿，那么任何容量的背包都有一個合法解“什么都不裝”，這個解的價值為0，所以初始時狀態的值也就全部為0了。

代碼在最前面已貼，不在此上傳。

一個常數優化

一維數組描述狀態時的偽代碼：

for i=1..N //枚舉物品
    for v=V..0 //枚舉容量，從大到小
        f[v]=max{f[v],f[v-weight[i]] + cost[i]};

觀察可知，對于第i個物品，枚舉背包容量下限時，可以到weight[i]為止。

原因：

1）對于第i物品，在求f[v]時，需要使用的狀態是 v ~ v -  weight[i] 這么多，這是由于v取最大容量V時，使用的狀態才是v - weight[i]，當v不取最大狀態時，使用的狀態肯定是在v ~ v -  weight[i]之間的。可以到weight[i]為止。

2）在到weight[i]為止時，還可以不進行if判斷，擔心v -  weight[i]是否越界

此時，偽代碼為

for i=1..N //枚舉物品
    for v=V..weight[i] //枚舉容量，從大到小
        f[v]=max{f[v],f[v-weight[i]] + cost[i]};

注意，對 f 數組，如果是檢測第i個物品是否能放入，0 ~ weight[i] - 1的這些位置是不會遍歷到的，則此時他們仍表示第i - 1次的狀態，即二維的f[i - 1][v]。

還可以繼續優化下界為

for i=1..N //枚舉物品
	bound=max{V-sum{weight[i..n]},weight[i]}//確定需要枚舉容量的下界
	for v=V..bound
		f[v]=max{f[v],f[v-weight[i]] + cost[i]};

原因：

1)網上的說法,不太懂,各位大牛可以指導下下。

對于第i次循環（指外循環），對于背包容量v = V(最大)時，對于f[v]的值，其實只要知道f[v-weight[i]]即可。以此類推，對于背包容量為 j 時，我們只需要知道到f[v-sum{weight[j..n]}]即可

2)還有人說

如果比v-sum{weight[j..n]}這個小，那么即使后面物品的全要也裝不滿背包。

所以對于物品i，小于v-sum{weight[j..n]}的v值，無意義。

總之是不懂。智商啊

作者說，當V很大是，效果好。

代碼

#include <iostream>
using namespace std;

const int N = 3;//物品個數
const int V = 5;//背包最大容量
int weight[N + 1] = {0,3,2,2};//物品重量
int value[N + 1] = {0,5,10,20};//物品價值

int f[V + 1] = {0};

int Max(int x,int y)
{
	return x > y ? x : y;
}

/*
目標：在不超過背包容量的情況下，最多能獲得多少價值

子問題狀態:f[j]:表示前i件物品放入容量為j的背包得到的最大價值

狀態轉移方程:f[j] = max{f[j],f[j - weight[i]] + value[i]}

初始化:f數組全設置為0
*/
int Knapsack()
{
	int sum = 0;//存儲還未處理物品的總容量
	int bound = 0;
	//初始化
	memset(f,0,sizeof(f));
	for (int i = 1;i <= N;i++)
	{
		sum += weight[i];
	}
	
	//遞推
	for (int i = 1;i <= N;i++) //枚舉物品
	{
		//設置下界
		if (i != 1)
		{
			sum -= weight[i - 1];
		}
		bound = Max(V - sum,weight[i]);

		for (int j = V;j >= bound;j--) //枚舉背包容量
		{
			if (f[j] < f[j - weight[i]] + value[i])
			{
				f[j] = f[j - weight[i]] + value[i];
			}
		}
	}
	return f[V];
}

int main()
{
	cout<<Knapsack()<<endl;
	system("pause");
	return 1;
}

 輸出方案

一般而言，背包問題是要求一個最優值，如果要求輸出這個最優值的方案，可以參照一般動態規劃問題輸出方案的方法：記錄下每個狀態的最優值是由狀態轉移方程的哪一項推出來的，換句話說，記錄下它是由哪一個策略推出來的。便可根據這條策略找到上一個狀態，從上一個狀態接著向前推即可。

這里我們首先給出01背包的二維狀態轉移方程

f[i][v] = max(f[i - 1][v],f[i - 1][v - weight[i]] + cost[i])

對于狀態f[i][v]，它來自兩種策略，可以是f[i - 1][v],也可以是f[i - 1][v - weight[i]] + cost[i]

其中，對于第二種情況，就是把物品i放入背包了，這里也是我們要找的情況

根據狀態轉移方程，我們可以給出兩種實現方法

1) 借助存儲狀態的數組，直接根據狀態轉移方程倒著推，檢測是否滿足

f[i][v] == f[i - 1][v - weight[i]] + value[i]

如果滿足，則把第i件物品放入了，此時我們要檢測第i - 1件物品，背包容量為v - weight[i]

不滿足則表示沒有把第i件物品放入，直接檢測第i - 1件物品，此時背包容量還是v

注意，這種方法只適用于存儲狀態數組不壓縮的情況。壓縮數組由于數據有覆蓋，不能使用

代碼

#include <iostream>
using namespace std;

const int N = 3;//物品個數
const int V = 5;//背包最大容量
int weight[N + 1] = {0,3,2,2};//物品重量
int value[N + 1] = {0,5,10,20};//物品價值

int f[N + 1][V + 1] = {{0}};

int Max(int x,int y)
{
	return x > y ? x : y;
}

/*
目標：在不超過背包容量的情況下，最多能獲得多少價值

子問題狀態:f[i][j]:表示前i件物品放入容量為j的背包得到的最大價值

狀態轉移方程:f[i][j] = max{f[i - 1][j],f[i - 1][j - weight[i]] + value[i]}

初始化:f數組全設置為0
*/
int Knapsack()
{
	//初始化
	memset(f,0,sizeof(f));
	//遞推
	for (int i = 1;i <= N;i++) //枚舉物品
	{
		for (int j = 1;j <= V;j++) //枚舉背包容量
		{
			f[i][j] = f[i - 1][j];
			if (j >= weight[i])
			{
				f[i][j] = Max(f[i - 1][j],f[i - 1][j - weight[i]] + value[i]);
			}
		}
	}
	return f[N][V];
}
/*
輸出順序:逆序輸出物品編號
注意：這里借助狀態數組f[i][v]
使用狀態轉移方程:f[i][j] = max{f[i - 1][j],f[i - 1][j - weight[i]] + value[i]}
*/
void PrintKnapsack()
{
	int i = N;//枚舉物品
	int j = V;//枚舉空間
	
	cout<<"加入背包的物品編號:"<<endl;
	while(i)
	{
		if (f[i][j] == f[i - 1][j - weight[i]] + value[i])
		{
			/*if不滿足，表示第i件物品沒裝入背包,
			  if條件滿足，表示放入背包了*/
			cout<<i<<" ";
			j -= weight[i];//此時容量減少
		}
		i--;
	}
	cout<<endl;
}

/*
輸出順序:順序輸出物品編號
注意：這里借助狀態數組f[i][v]
使用狀態轉移方程:f[i][j] = max{f[i - 1][j],f[i - 1][j - weight[i]] + value[i]}
*/
void PrintKnapsack_recursion(int i,int j)
{
	if (i == 0 || j == 0)
	{
		return;
	}
	if (f[i][j] == f[i - 1][j - weight[i]] + value[i])
	{
		PrintKnapsack_recursion(i - 1,j - weight[i]);
		cout<<i<<" ";
	}
}

int main()
{
	cout<<Knapsack()<<endl;
	PrintKnapsack();
	PrintKnapsack_recursion(N,V);
	system("pause");
	return 1;
}

2) 另外開辟數組，在求解最大收益時做標記位。求解完最大收益后，根據這個新數組倒著推結果

思想：對于現在這個狀態的位置，它存儲的是該狀態上一位置

注意：這種方法均適用存儲狀態數組不壓縮 和 壓縮兩種情況

代碼：

#include <iostream>
using namespace std;

const int N = 3;//物品個數
const int V = 5;//背包最大容量
int weight[N + 1] = {0,3,2,2};//物品重量
int value[N + 1] = {0,5,10,20};//物品價值

int f[V + 1] = {0};

int G[N + 1][V + 1] = {{0}};//求背包序列

int Max(int x,int y)
{
	return x > y ? x : y;
}

/*
目標：在不超過背包容量的情況下，最多能獲得多少價值

子問題狀態:f[j]:表示前i件物品放入容量為j的背包得到的最大價值

狀態轉移方程:f[j] = max{f[j],f[j - weight[i]] + value[i]}

初始化:f數組全設置為0
*/
int Knapsack()
{
	//初始化
	memset(f,0,sizeof(f));
	memset(G,0,sizeof(G));
	//遞推
	for (int i = 1;i <= N;i++) //枚舉物品
	{
		for (int j = V;j >= weight[i];j--) //枚舉背包容量
		{
			if (f[j] < f[j - weight[i]] + value[i])
			{
				f[j] = f[j - weight[i]] + value[i];
				G[i][j] = 1;
			}
		}
	}
	return f[V];
}
/*
輸出順序:逆序輸出物品編號
注意：這里另外開辟數組G[i][v],標記上一個狀態的位置
G[i][v] = 1:表示物品i放入背包了，上一狀態為G[i - 1][v - weight[i]]
G[i][v] = 0:表示物品i沒有放入背包，上一狀態為G[i - 1][v]
*/
void PrintKnapsack()
{
	int i = N;//枚舉物品
	int j = V;//枚舉空間
	
	cout<<"加入背包的物品編號:"<<endl;
	while(i)
	{
		if (G[i][j] == 1)
		{
			/*if不滿足，表示第i件物品沒裝入背包,
			  if條件滿足，表示放入背包了*/
			cout<<i<<" ";
			j -= weight[i];//此時容量減少
		}
		i--;
	}
	cout<<endl;
}

/*
輸出順序:順序輸出物品編號
注意：這里另外開辟數組G[i][v],標記上一個狀態的位置
G[i][v] = 1:表示物品i放入背包了，上一狀態為G[i - 1][v - weight[i]]
G[i][v] = 0:表示物品i沒有放入背包，上一狀態為G[i - 1][v]
*/
void PrintKnapsack_recursion(int i,int j)
{
	if (i == 0 || j == 0)
	{
		return;
	}
	if (G[i][j] == 1)
	{
		PrintKnapsack_recursion(i - 1,j - weight[i]);
		cout<<i<<" ";
	}
}

int main()
{
	cout<<Knapsack()<<endl;
	PrintKnapsack();
	PrintKnapsack_recursion(N,V);
	system("pause");
	return 1;
}

小結：

01 背包問題是最基本的背包問題，它包含了背包問題中設計狀態、方程的最基本思想。另外，別的類型的背包問題往往也可以轉換成01 背包問題求解。故一定要仔細體會上面基本思路的得出方法，狀態轉移方程的意義，以及空間復雜度怎樣被優化。