狄拉克δ函數(shù)探源:從廣義函數(shù)到分析核與信號(hào)窗 (AI輔助撰寫(xiě))
本文由AI輔助撰寫(xiě),主體寫(xiě)作為AI,行文思路本人提供。
本人對(duì)AI輔助寫(xiě)作的博客的評(píng)論、吐槽與糾正均以類似本段的引用格式來(lái)說(shuō)明。
(AI寫(xiě)的真有些料,但也是真的狗屁不通,下面第五點(diǎn)的行文就很令人迷惑)
狄拉克\(\delta\)函數(shù)探源:從廣義函數(shù)到分析核與信號(hào)窗
1. “理想”卻“不存在”的脈沖
在許多科學(xué)和工程領(lǐng)域,狄拉克\(\delta\)函數(shù)(Dirac Delta Function)是一個(gè)不可或缺的工具。我們通常期望它是一個(gè)“函數(shù)”\(\delta(t)\),并滿足以下三個(gè)理想屬性:
- 無(wú)限集中: 當(dāng) \(t \neq 0\) 時(shí), \(\delta(t) = 0\)。
- 無(wú)限尖銳: 當(dāng) \(t = 0\) 時(shí), \(\delta(t) = \infty\)。
- 能量歸一: \(\int_{-\infty}^{\infty} \delta(t) dt = 1\)。
這個(gè)定義的便利性在于其完美的“篩選特性”(Sifting Property):
它代表了一個(gè)瞬時(shí)的、能量歸一化的“單位脈沖”。
然而,從嚴(yán)格的數(shù)學(xué)函數(shù)定義來(lái)看,滿足條件1和2的函數(shù)其積分為0,這與條件3矛盾。因此,\(\delta(t)\)并不是一個(gè)傳統(tǒng)意義上的函數(shù)。
畢竟,單點(diǎn)處的值不影響積分的結(jié)果,那么0處的值也不影響總積分結(jié)果才對(duì)。
但正常在學(xué)習(xí)沖激函數(shù)時(shí)采用的理解方式是完全合理的,接下來(lái)就要解釋其合理性了。
那么,我們?cè)撊绾螄?yán)謹(jǐn)?shù)乩斫夂褪褂盟兀?/p>
2. 數(shù)學(xué)的嚴(yán)謹(jǐn)化:作為極限的\(\delta\)函數(shù)(狄拉克序列)
數(shù)學(xué)上,\(\delta\)函數(shù)被視為一種“廣義函數(shù)”或“分布”(Distribution)。一個(gè)更直觀且在分析中被廣泛采用的理解是:\(\delta\)函數(shù)是一個(gè)函數(shù)序列 \(\{ \delta_N(t) \}\) 在 \(N \to \infty\) 時(shí)的極限(在分布的意義下)。
這個(gè)序列,我們稱之為“狄拉克序列”(Dirac Sequence),必須滿足特定的條件才能在極限狀態(tài)下模擬\(\delta\)函數(shù)的篩選特性。
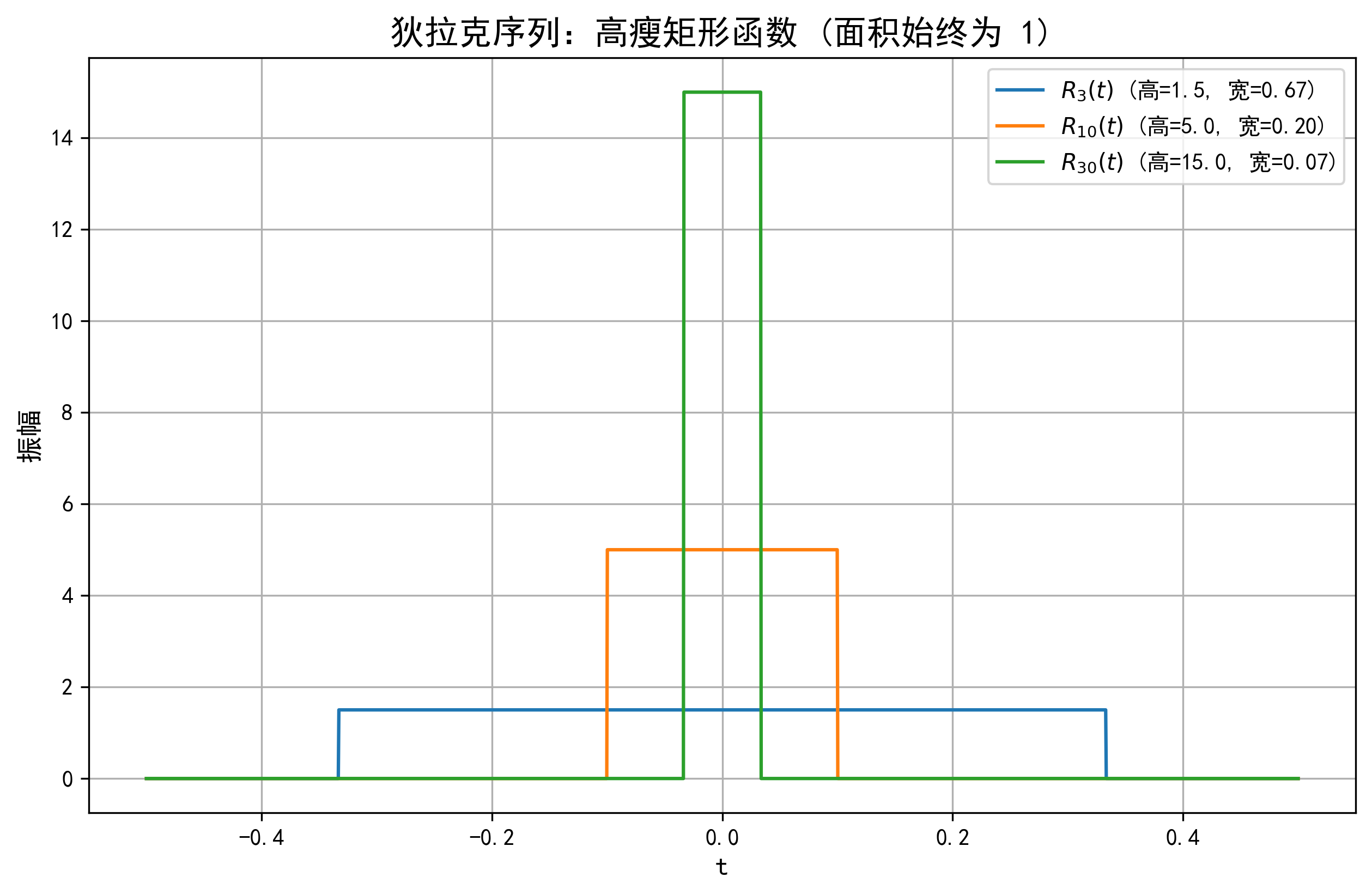
示例 1:高瘦矩形序列 (最經(jīng)典的入門(mén)模型)
這正是最常用于介紹\(\delta\)函數(shù)的模型。我們定義一個(gè)矩形函數(shù)序列 \(R_N(t)\)(在一些文獻(xiàn)中也寫(xiě)作 \(\Pi_N(t)\)):
這個(gè)函數(shù)族:
- 面積歸一: \(\int_{-\infty}^{\infty} R_N(t) dt = (\text{高度 } N/2) \times (\text{寬度 } 2/N) = 1\)。
- 極限集中: 當(dāng) \(N \to \infty\),寬度 \(2/N \to 0\),而高度 \(N/2 \to \infty\)。
雖然大多數(shù)課程并不會(huì)嚴(yán)格定義δ函數(shù),但講述時(shí)采用的思路卻能確實(shí)定義好δ函數(shù)。
不過(guò)不知道大家學(xué)習(xí)時(shí)是否有這個(gè)疑問(wèn):真的只有這種趨近嗎,還有別的函數(shù)能趨近成沖激函數(shù)嗎?
接下來(lái)就介紹了一些其它的趨近方式。如果有興趣可以計(jì)算一下,在 \(N \to \infty\) 時(shí),其本身與其傅里葉變換是否分別趨近于沖激函數(shù)和常數(shù)(答案顯然是肯定的)??
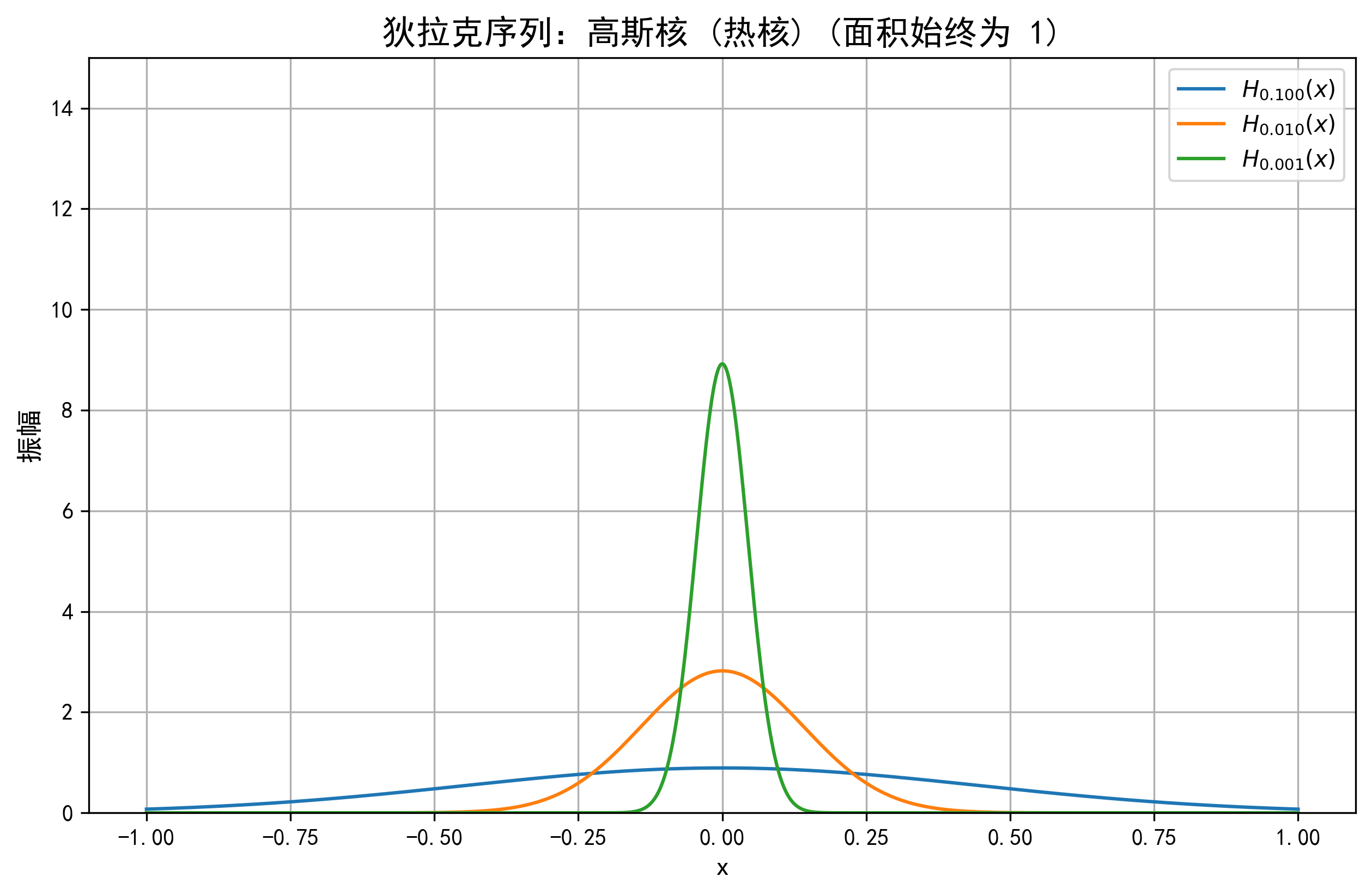
示例 2:高斯函數(shù)(熱核)
另一個(gè)重要的例子是高斯函數(shù)(在物理中也稱為熱核, Heat Kernel):
這里我們用 \(t \to 0^+\) 來(lái)代替 \(N \to \infty\)。當(dāng) \(t \to 0^+\) 時(shí),這個(gè)函數(shù)的高度 \(\to \infty\),寬度 \(\to 0\),并且其全域積分始終為1。它也是\(\delta\)函數(shù)的一個(gè)完美代表。
這里的高斯函數(shù)還有挺多的性質(zhì)的。比如,\(t=\frac{1}{2}\)時(shí)它是傅里葉變換的特征函數(shù),特征值為1。
特征函數(shù)類比線代的特征向量。在線代中,我們稱 \(Ax=\lambda x\) 中 \(x\) 為特征向量,\(\lambda\)為特征值。在這里,我們有 \(\mathcal{F}(H_{\frac{1}{2}}(x)) = 1 \cdot H_{\frac{1}{2}}(x)\)
事實(shí)上,對(duì)于任意符合傅里葉變換的基礎(chǔ)條件的函數(shù),其理論上均可分解為厄米函數(shù) \(\psi_n(x)=C_n H_n(x) e^{-x^2}\) 的和(此處 \(H_n(x) \equiv (- 1)^n \mathrm{e} ^{x^2} \frac{\mathrmw0obha2h00^{n}}{\mathrmw0obha2h00{x}^{n}} \left( \mathrm{e} ^{-x^2} \right)\)是厄米多項(xiàng)式,前三項(xiàng)分別為 \(1, 2x, 4x^2-2\)。由于本文其它地方不會(huì)出現(xiàn)該多項(xiàng)式,因此此處做特殊說(shuō)明,本文其它地方的\(H_n\)均指高斯函數(shù)),從而可以通過(guò)特征值來(lái)簡(jiǎn)單求解傅里葉變換后的值。實(shí)際上大多數(shù)時(shí)候我們根本求不出來(lái)(樂(lè))
\(t=\frac{1}{2}\)時(shí)的高斯函數(shù)我們后面還會(huì)提到。
3. 傅里葉分析中的“核函數(shù)”
這種“狄拉克序列”在傅里葉分析中有另一個(gè)名字:“核函數(shù)”(Kernels)。
在分析學(xué)中,我們不直接處理 \(\delta(t)\),而是處理這些核函數(shù)。我們的目標(biāo)是證明一個(gè)函數(shù) \(f\) 可以由其傅里葉級(jí)數(shù)(或變換)重構(gòu)。實(shí)現(xiàn)這一點(diǎn)的關(guān)鍵工具是卷積。我們希望證明:
(在數(shù)學(xué)上,卷積 \(f * \delta = f\),所以 \(K_N\) 序列在極限意義下就是卷積運(yùn)算的“單位元”,即\(\delta\)函數(shù))。
滿足這個(gè)條件的序列 \(K_N\) 被稱為“好核”(Good Kernels)。一個(gè)序列成為“好核”,必須(大致)具備三個(gè)關(guān)鍵屬性(以周期情況為例):
- 質(zhì)量歸一化: \(\frac{1}{2\pi}\int_{-\pi}^{\pi} K_N(t)dt = 1\)。
- 質(zhì)量集中: 隨著 \(N \to \infty\),所有的質(zhì)量(面積)都必須集中在原點(diǎn)附近。
- 總質(zhì)量有界: \(\int_{-\pi}^{\pi} |K_N(t)| dt \le M\)。
一個(gè)更強(qiáng)的、通常也更“好”的屬性是正定性:\(K_N(t) \ge 0\),這個(gè)屬性自動(dòng)保證了條件1和3等價(jià)。
在傅里葉級(jí)數(shù)的研究中,我們立即遇到了幾個(gè)核心的核函數(shù):
核函數(shù) 1:狄利克雷核 (Dirichlet Kernel)
這是傅里葉級(jí)數(shù)標(biāo)準(zhǔn)部分和 \(S_N(f) = \sum_{n=-N}^N \hat{f}(n) e^{int}\) 對(duì)應(yīng)的核。
狄利克雷核是壞的(Bad Kernel)!它滿足條件1和2,但嚴(yán)重違反了條件3。它的 \(L^1\) 范數(shù)會(huì)隨著 \(N\) 增大而趨于對(duì)數(shù)無(wú)窮(\(\int |D_N| \approx c \log N\))。更直觀地說(shuō),它不是正定的,它有劇烈的震蕩和大量的負(fù)“旁瓣”。
\(\delta(x)\)的傅里葉級(jí)數(shù)是無(wú)窮長(zhǎng)的,我們截取有限區(qū)間的頻率,忽略高頻后做傅里葉逆變換就是\(D_N(t)\)
核函數(shù) 2:費(fèi)耶核 (Fejér Kernel)
這是切薩羅求和(Cesàro summability,即部分和的平均) \(\sigma_N(f)\) 對(duì)應(yīng)的核。
費(fèi)耶核是好的(Good Kernel)。它滿足所有三個(gè)條件,尤其是,它是正定的(\(F_N(t) \ge 0\)),因此其 \(L^1\) 范數(shù)恒為1。
切薩羅和是 \(\sigma_N = \frac{ \sum_{i=1}^{N} S_i}{N}\)。對(duì)于收斂數(shù)列,在\(N \to \infty\)時(shí),n較大項(xiàng)更多,取值接近\(N \to \infty\)時(shí)取值的也更多,從而最終切薩羅和與正常的無(wú)窮和是一致的。切薩羅和同時(shí)也能求部分發(fā)散數(shù)列,使得頻譜不收斂的也能成功求和。
核函數(shù) 3:泊松核 (Poisson Kernel)
這是阿貝爾求和(Abel summability)\(A_r(f)\) 對(duì)應(yīng)的核。
這(在 \(r \to 1^-\) 的極限下)也是一個(gè)非常好的(Good Kernel)。它也是正定的,且積分為1。
核函數(shù) 4:高斯核(熱核)(Gaussian / Heat Kernel)
這個(gè)核 \(H_t(x)\) 在示例2中已經(jīng)提到。這(在 \(t \to 0^+\) 的極限下)也是一個(gè)好的(Good Kernel),它積分為1,正定,并且質(zhì)量在 \(t \to 0\) 時(shí)高度集中。
總結(jié)一下:
- 壞核 (Bad Kernel): 狄利克雷核 (\(D_N\))。
- 好核 (Good Kernels): 費(fèi)耶核 (\(F_N\))、泊松核 (\(P_r\))、高斯/熱核 (\(H_t\)),以及我們最早的矩形序列 \(R_N(t)\)。
4. 現(xiàn)實(shí)世界的妥協(xié):從“核”到“窗”
這一段寫(xiě)的有點(diǎn)怪,不過(guò)也還行吧,就用這版了。
這一段的緣起是窗的形式與前面核有些類似,但是讓AI自由發(fā)揮的結(jié)果很糟糕。不過(guò)這一版至少?zèng)]有什么明顯的邏輯問(wèn)題。
在深入之前,我們必須澄清一個(gè)關(guān)鍵概念。在信號(hào)處理(DSP)的標(biāo)準(zhǔn)流程中,“窗函數(shù)” (Window Function) 通常是指一個(gè)在時(shí)域 (Time Domain) 上有限長(zhǎng)的函數(shù) \(w(t)\),我們用它來(lái)截取一個(gè)(理論上無(wú)限長(zhǎng)的)信號(hào) \(f(t)\),以便進(jìn)行傅里葉變換(例如DFT/FFT):
這樣做的后果是,在頻域中,我們得到的不再是 \(f(t)\) 真實(shí)的頻譜 \(\hat{f}(\xi)\),而是 \(\hat{f}(\xi)\) 與窗函數(shù)自身的傅里葉變換 \(\hat{w}(\xi)\) 的卷積:
在這個(gè)標(biāo)準(zhǔn)流程中,我們用來(lái)卷積的“核”是 \(\hat{w}(\xi)\),它位于頻域。
這里寫(xiě)的說(shuō)實(shí)話有點(diǎn)糟糕,看看就行了,看不懂也沒(méi)關(guān)系。
一般的窗是時(shí)域乘積頻域卷積,而我們前面提到的核是時(shí)域卷積頻域乘積。不知道怎么給AI寫(xiě)成這樣了。但至少我們可以看到窗函數(shù)和核函數(shù)的形式上的類似了。
而我們這里(從傅里葉級(jí)數(shù)出發(fā))的視角是對(duì)偶(Dual)的:
我們有一個(gè)無(wú)限的系數(shù)序列 \(\hat{f}(n)\),我們必須在頻域將其截?cái)唷?/p>
窗函數(shù) 1:矩形窗 (Rectangular Window / Boxcar)
計(jì)算標(biāo)準(zhǔn)部分和 \(S_N(f)\),等價(jià)于在頻域乘以一個(gè)矩形窗:
根據(jù)卷積定理,這個(gè)操作(頻域乘矩形窗)等價(jià)于在時(shí)域卷積了狄利克雷核 \(D_N(t)\)。
窗函數(shù) 2:三角窗 (Triangular / Bartlett Window)
計(jì)算切薩羅求和 \(\sigma_N(f)\),等價(jià)于在頻域乘以一個(gè)三角窗:
這個(gè)操作(頻域乘三角窗)等價(jià)于在時(shí)域卷積了費(fèi)耶核 \(F_N(t)\)。
結(jié)論: 我們的討論,是從傅里葉級(jí)數(shù)出發(fā),研究了時(shí)域上的核函數(shù)(\(D_N, F_N\))。這與DSP中“時(shí)域加窗,頻域卷核”的視角是對(duì)偶的。但它們是同一個(gè)數(shù)學(xué)問(wèn)題的兩個(gè)側(cè)面:\(D_N(t)\) 是 \(W_{Rect}(n)\) 的變換核, \(F_N(t)\) 是 \(W_{Tri}(n)\) 的變換核。
5. 工程的權(quán)衡:分辨率 vs. 頻譜泄露
哈哈
前面那段寫(xiě)的確實(shí)不行,這里寫(xiě)的也有點(diǎn)亂,主旁瓣的矛盾為什么存在,這和核為什么有關(guān)系,這些都沒(méi)有提。這部分可以直接跳過(guò)了。
這部分AI寫(xiě)的也太爛了。
這個(gè)對(duì)偶關(guān)系,恰好讓我們能從核函數(shù)的數(shù)學(xué)性質(zhì)(好/壞)來(lái)理解窗函數(shù)的工程表現(xiàn)。
為什么工程師們?nèi)绱擞憛捑匦未埃恳驗(yàn)樗鼘?duì)應(yīng)的核 \(D_N(t)\) 是個(gè)“壞核”,它有巨大的負(fù)旁瓣。在信號(hào)處理中,這些旁瓣被稱為頻譜泄露 (Spectral Leakage)。
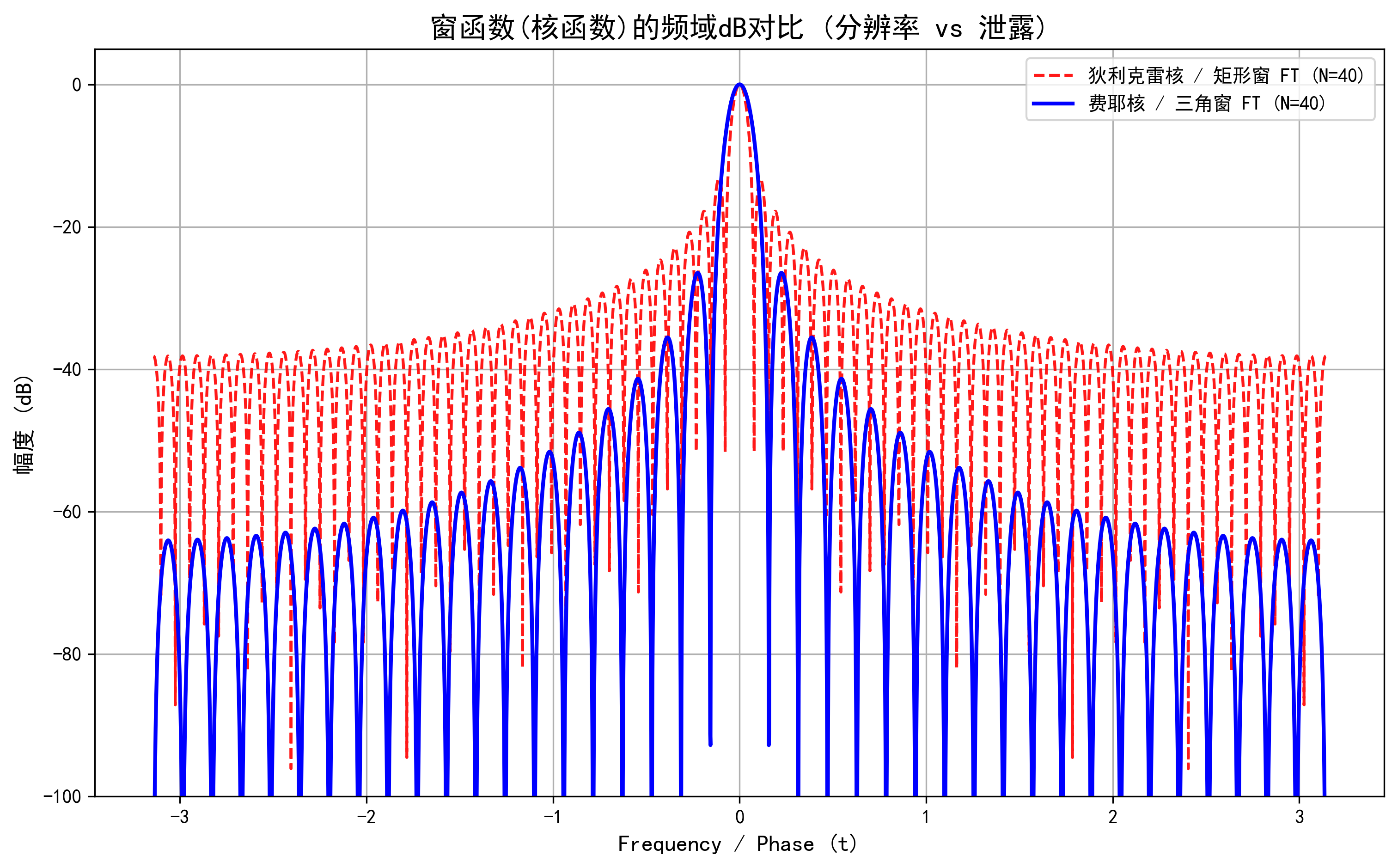
在頻域(我們直接觀察 \(D_N\) 和 \(F_N\) 的圖像):
- 主瓣(Main Lobe)寬度 決定了我們的頻率分辨率。主瓣越窄,我們?cè)侥軈^(qū)分兩個(gè)靠得很近的頻率。
- 旁瓣(Sidelobes)高度 決定了頻譜泄露。如果旁瓣很高,一個(gè)非常強(qiáng)的信號(hào)會(huì)通過(guò)它的旁瓣“泄露”能量到其他頻率點(diǎn)上,把我們真正想聽(tīng)的微弱信號(hào)給完全淹沒(méi)了。
“好核”的數(shù)學(xué)性質(zhì)(正定性)和“好窗函數(shù)”的工程性質(zhì)(低旁瓣/低泄露)在這里完美地統(tǒng)一了!
- 狄利克雷核/矩形窗: 壞核。主瓣最窄(分辨率最高),但旁瓣最高(泄露最嚴(yán)重)。
- 費(fèi)耶核/三角窗: 好核。旁瓣極低(泄露小,因?yàn)樗钦ǖ模靼陮捔撕芏啵ǚ直媛什睿?/li>
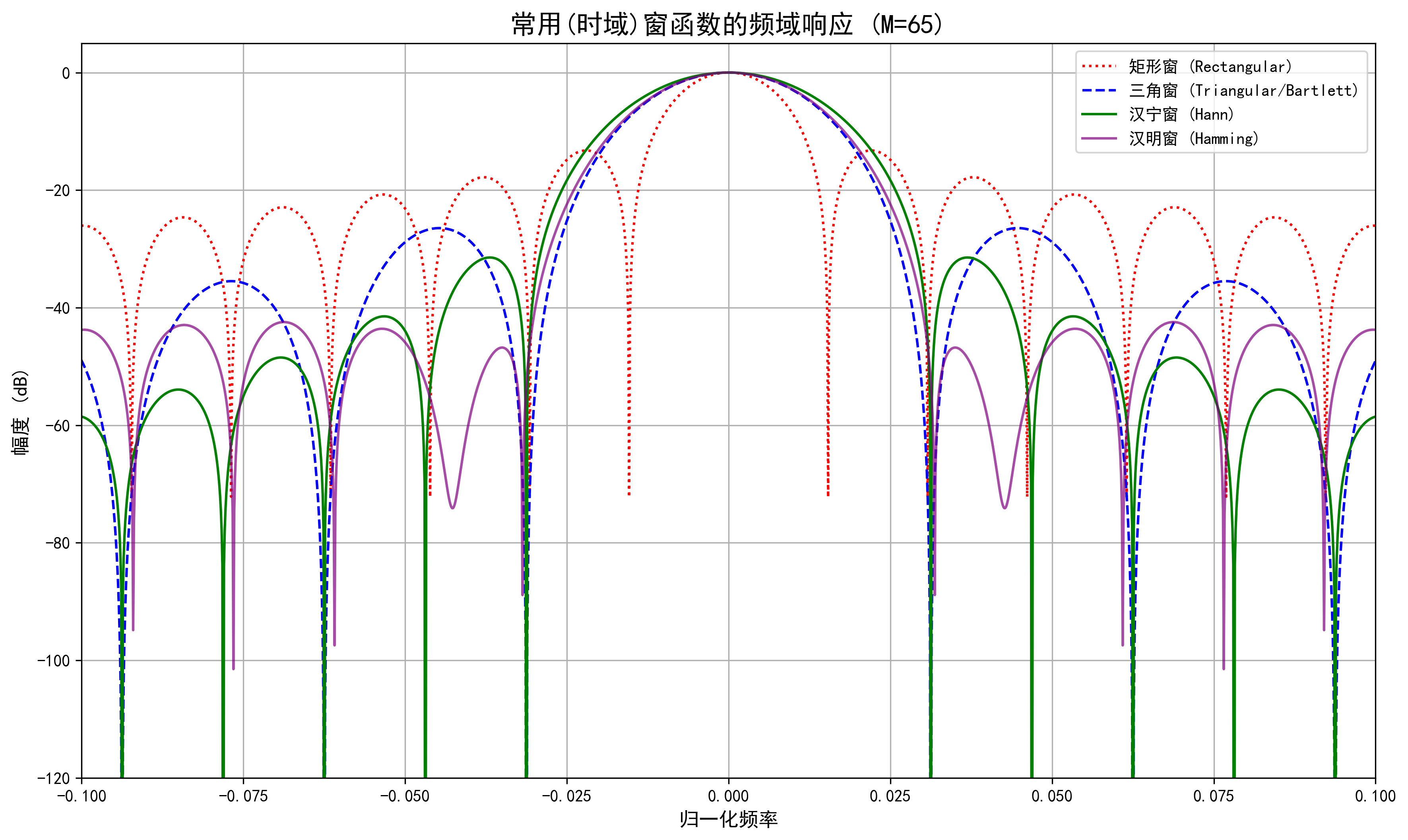
更多常用窗函數(shù)
工程師們?yōu)榱似胶膺@對(duì)矛盾,發(fā)明了更多的(時(shí)域)窗函數(shù)。它們(在頻域應(yīng)用時(shí))都對(duì)應(yīng)著不同的(通常是“好”的)核函數(shù):
- 漢寧窗 (Hann Window): \(w(t) = 0.5 \left( 1 - \cos\left(\frac{2\pi t}{T}\right) \right)\)
- 漢明窗 (Hamming Window): \(w(t) = 0.54 - 0.46 \cos\left(\frac{2\pi t}{T}\right)\)
- 布萊克曼窗 (Blackman Window): \(w(t) = 0.42 - 0.5 \cos\left(\frac{2\pi t}{T}\right) + 0.08 \cos\left(\frac{4\pi t}{T}\right)\)
- ...(均在 \(0 \le t \le T\) 內(nèi),T為窗口寬度)
這些窗函數(shù)提供了比三角窗更好的旁瓣抑制(更低的泄露),同時(shí)主瓣寬度又比三角窗更窄(更好的分辨率)。
6. 無(wú)法兩全的宿命:核函數(shù)與海森堡不確定性原理
是的,就是那個(gè)海森堡不確定性原理,量子力學(xué)的那個(gè)。十分推薦看Stein大佬的Fourier Analysis: An Introduction,對(duì)這里有不錯(cuò)的論述。
它與傅里葉變換的放縮有很大的關(guān)系,我們?cè)谶@里使用核函數(shù)來(lái)展現(xiàn)其關(guān)系。
在前面的討論中,我們看到了“好核”(如費(fèi)耶核 \(F_N\))和“壞核”(如狄利克雷核 \(D_N\))在工程應(yīng)用(窗函數(shù))中如何表現(xiàn)為“低泄露/低分辨率”和“高泄露/高分辨率”的權(quán)衡。
但為什么必須存在這種權(quán)衡呢?為什么我們不能設(shè)計(jì)一個(gè)“完美”的核,它在時(shí)域(或頻域)既無(wú)限窄(分辨率高),又沒(méi)有旁瓣(無(wú)泄露)?
答案是:因?yàn)橐粋€(gè)更深刻的數(shù)學(xué)定律禁止了這一點(diǎn)。這個(gè)定律就是不確定性原理。
讓我們從核函數(shù)的角度來(lái)理解。\(\delta\)函數(shù)本身是這個(gè)原理的極端體現(xiàn):
- 理想 \(\delta(t)\) 函數(shù) (時(shí)域): 寬度 = 0 (無(wú)限集中)。
- 傅里葉變換: \(1(\xi)\) (常數(shù)1) (頻域): 寬度 = \(\infty\) (無(wú)限分散)。
- 常數(shù)函數(shù) \(f(t)=1\) (時(shí)域): 寬度 = \(\infty\) (無(wú)限分散)。
- 傅里葉變換: \(\delta(\xi)\) (頻域): 寬度 = 0 (無(wú)限集中)。
這揭示了一個(gè)真理:一個(gè)函數(shù)在時(shí)域(或空域)上越集中(越窄),它的傅里葉變換在頻域上就越分散(越寬)。反之亦然。
我們來(lái)看看我們已經(jīng)討論過(guò)的核函數(shù)是如何體現(xiàn)這一點(diǎn)的:
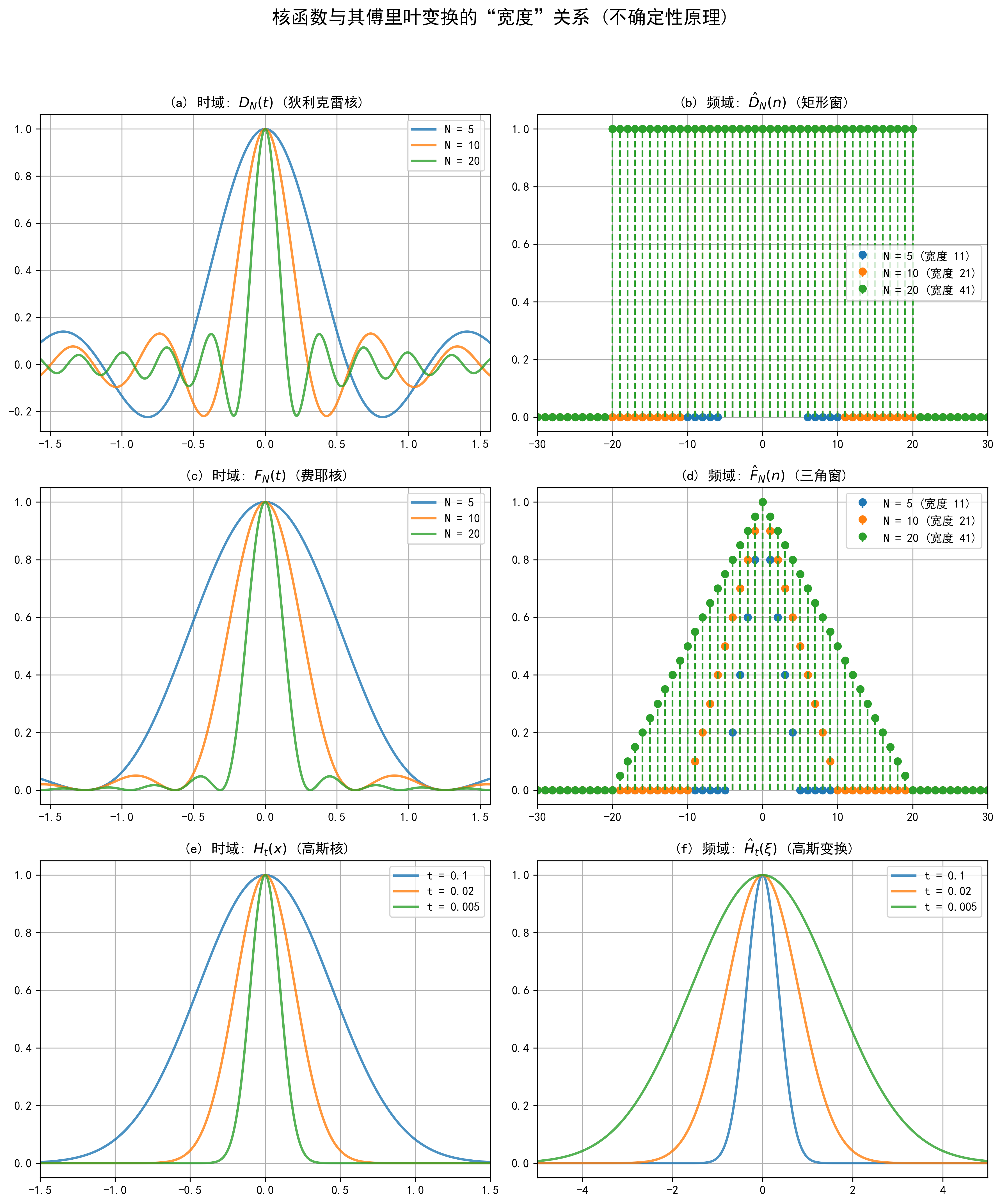
觀察上圖(圖片7),我們發(fā)現(xiàn):
- 時(shí)域(核函數(shù) \(K_N(t)\)): 無(wú)論是 \(D_N(t)\)、\(F_N(t)\) 還是 \(H_t(x)\),當(dāng) \(N \to \infty\) (或 \(t \to 0\)) 時(shí),它們?cè)?strong>時(shí)域都變得越來(lái)越集中(寬度 \(\to 0\))。
- 頻域(變換 \(\hat{K}_N(n)\)):
- \(D_N(t)\) 的傅里葉變換(系數(shù))是 \(W_{Rect}(n)\),其寬度為 \(2N+1\)。
- \(F_N(t)\) 的傅里葉變換(系數(shù))是 \(W_{Tri}(n)\),其寬度為 \(2N+1\)。
- \(H_t(x)\) 的傅里葉變換是 \(\hat{H}_t(\xi) = e^{-4\pi^2 t \xi^2}\),其寬度與 \(1/\sqrt{t}\) 成正比。
雖然咱看不出來(lái)這些,至少咱能看出來(lái)時(shí)域上越來(lái)越尖瘦了,頻域上則越來(lái)越寬且趨近于取值全1了
結(jié)論是:當(dāng)我們讓核函數(shù)在時(shí)域上越來(lái)越集中(\(N \to \infty\) 或 \(t \to 0\))時(shí),它們的傅里葉變換(即它們?cè)陬l域的形態(tài))必然變得越來(lái)越分散(寬度 \(\to \infty\))。
一個(gè)函數(shù)和它的傅里葉變換不能同時(shí)被任意地“壓縮”。
這就是海森堡不確定性原理(Heisenberg uncertainty principle)的數(shù)學(xué)本質(zhì)。如果我們用方差(Variance)來(lái)衡量一個(gè)歸一化函數(shù) \(\psi(x)\) 及其變換 \(\hat{\psi}(\xi)\) 的“寬度”或“集中度”:
那么它們二者的乘積必然有一個(gè)嚴(yán)格的下限:
這里的“傅里葉變換的定義”是指時(shí)域角頻率還是頻率。使用頻率時(shí)是上面提到的 \(\frac{1}{4\pi}\),使用角頻率(量子力學(xué)一般用這個(gè))則是 \(\frac{1}{2}\)
在所有函數(shù)中,只有高斯函數(shù)(即我們的熱核 \(H_t(x)\))能夠取到這個(gè)不等式的最小值。從這個(gè)意義上說(shuō),高斯核是在時(shí)域集中度和頻域集中度之間做出了“最好”權(quán)衡的核函數(shù)。
這個(gè)純粹的數(shù)學(xué)定律,在量子力學(xué)中成為了基石。因?yàn)橐粋€(gè)粒子的動(dòng)量波函數(shù)恰好是其位置波函數(shù)(通過(guò)普朗克常數(shù)關(guān)聯(lián))的傅里葉變換。因此,這個(gè)數(shù)學(xué)限制直接導(dǎo)致了物理定律:我們無(wú)法同時(shí)精確測(cè)量一個(gè)粒子的位置(壓縮 \(\Delta x\))和它的動(dòng)量(壓縮 \(\Delta p\))。
其實(shí)還差一個(gè) \(\sqrt{\hbar}\),角頻率下傅里葉變換需要對(duì)稱要在積分前乘上常數(shù) \(\frac{1}{\sqrt{2\pi}}\),量子力學(xué)里則是 \(\frac{1}{\sqrt{2\pi\hbar}}\),并在后續(xù)的傅里葉變換公式內(nèi)的 \(e\) 的次方上做修改:\(e^{ipx/\hbar}\)(其實(shí)就是動(dòng)量和位置都除了個(gè)普朗克常數(shù)\(\hbar\)罷了:D
下面的推導(dǎo)個(gè)人不是很理解,但AI說(shuō)了那就是吧,這個(gè)應(yīng)該和海森堡不確定性原理沒(méi)啥關(guān)系
回到我們的分析中:
- 狄利克雷核 \(D_N(t)\)(Sinc函數(shù))之所以在工程上表現(xiàn)不佳(高旁瓣/泄露),正是因?yàn)樗陬l域的“窗”(矩形窗)是“尖銳”的(不連續(xù)的)。這種時(shí)域(或頻域)的突變,必然導(dǎo)致其變換域的無(wú)限分散(Sinc函數(shù) \(1/t\) 的緩慢衰減)。
- 費(fèi)耶核 \(F_N(t)\)(Sinc平方函數(shù))之所以表現(xiàn)更好(低旁瓣/泄露),是因?yàn)樗陬l域的“窗”(三角窗)是連續(xù)且平滑的。這種平滑性允許其變換域(時(shí)域)的能量更集中(\(1/t^2\) 的快速衰減)。
最終,我們對(duì) \(\delta\) 函數(shù)的所有近似(無(wú)論是數(shù)學(xué)家稱的“核”還是工程師稱的“窗”),都受制于這個(gè)根本的不確定性原理。
參考文獻(xiàn)與鏈接
如果是學(xué)信號(hào)與系統(tǒng)的同學(xué),很推薦去看看Stein的Fourier Analysis: An Introduction,不用讀完,看到二維的傅里葉分析之前就行,對(duì)理解很有幫助。
小時(shí)百科上對(duì)狄拉克函數(shù)的嚴(yán)謹(jǐn)定義則是寫(xiě)本文的緣由。如果沒(méi)有那個(gè)嚴(yán)謹(jǐn)定義也不會(huì)有類似散文一樣有想到哪寫(xiě)到哪的行文思路的本文。
- Stein, E. M., & Shakarchi, R. (2003). Fourier Analysis: An Introduction. Princeton University Press.
- 小時(shí)百科 (wuli.wiki). (n.d.). Delta 函數(shù). https://wuli.wiki/online/Delta.html
本文來(lái)自博客園,轉(zhuǎn)載請(qǐng)注明原文鏈接:http://www.rzrgm.cn/0q1e/p/19103119/dirac_and_uncertainty





 浙公網(wǎng)安備 33010602011771號(hào)
浙公網(wǎng)安備 33010602011771號(hào)