一點記錄罷了（

寫在前面：

感覺我有個毛病，寫一段時間的題就會不自覺地減緩效率，有點擺爛（尤其晚上），寫點總結(jié)吧，利用一下時間并養(yǎng)成好的習(xí)慣

---

2025/07/16

今天如幾天常在樓下聽 stntn 學(xué)長講課，簡單附屬一下內(nèi)容：

• kruskal重構(gòu)樹：

挺簡單的一個trick，對于一個關(guān)于樹上特定邊權(quán)的問題，可以先搞一遍最小生成樹，排序從大到小的邊權(quán)，通過并查集搞出一棵搜索樹
這個搜索樹性質(zhì)是對于任意重構(gòu)樹葉子兩點，原樹上該兩點的簡單路徑中邊權(quán)最大值就是重構(gòu)樹的LCA的值
P1967 [NOIP 2013 提高組] 貨車運(yùn)輸：
裸題，搞出重構(gòu)樹找LCA即可

P7834 [ONTAK2010] Peaks 加強(qiáng)版：
重構(gòu)樹向上找不超過x的LCA，在該LCA的子樹上搞主席樹求區(qū)間kth，碼量挺大的，還沒調(diào)出來（

P4768 [NOI2018] 歸程：
在重構(gòu)樹定值LCA的子樹結(jié)點上移動不需要花費(fèi)，優(yōu)化了時間

• 分層圖最短路

挺版的，看到不好建邊的時候，把后面的圖拷貝一份，再將該點連向這張圖，主要是讓最短路好跑一些
P4568 [JLOI2011] 飛行路線
:看到免費(fèi)的航線不好轉(zhuǎn)移，考慮分層圖，最多做10次免費(fèi)飛機(jī)，把原圖拷貝k次，每個點u有向下一層v的免費(fèi)邊，也有向這一層v的正常邊，跑最短路即可
P3831 [SHOI2012] 回家的路：
網(wǎng)格圖上只有特定點可以轉(zhuǎn)向，考慮將網(wǎng)格變成只有橫著走與只有豎著走兩張圖，特定點可從橫向圖轉(zhuǎn)到豎向圖/豎向圖轉(zhuǎn)到橫向圖，起點終點最短路，注意空間，所以要縮點，只存有用的點

• 2-SAT 問題

挺簡單的，畢竟花時間自習(xí)過，對于各種\(0/1\)變量的共存問題，對每個必要狀態(tài)連邊，作tarjan找環(huán)，如果一點的兩個狀態(tài)在同一環(huán)上（又要存在，又要不存在），即可判斷無解
P4782 【模板】2-SAT：
真的純板子，就按照上方說法寫就完了
CF1697F Too Many Constraints
每個點拆成多個bool變量，然后建邊即可，重要的是要看出來要用2-SAT 解決

• 建圖優(yōu)化

講了個前綴和優(yōu)化建圖，沒聽大明白，但網(wǎng)上好像沒有講這個的，感覺不是很重要，先擱置吧，掛個例題P6378 [PA 2010] Riddle
還有個線段樹優(yōu)化建圖，把板子敲了，挺版的（CF786B Legacy

• 總結(jié)

題見少了，調(diào)代碼跳少了，一道藍(lán)題卡了半個下午，發(fā)現(xiàn)只是小錯誤（

2025/07/17

怎么上午就開始總結(jié)了（汗
如常上午 stntn 講課，接著掛上聽課記錄吧

• 分塊

這方面之前學(xué)過，不再從頭講述了，可以去看之前的分塊筆記Link

• 勢能分析

dottle剛講過，就是一種分析復(fù)雜度的方法，分析完了就可以放心去寫暴力了
搭配那幾道分塊食用
簡單來說,就是把復(fù)雜度拆成兩個部分,一個是原序列做完產(chǎn)生的復(fù)雜,一個是新加入玩意的復(fù)雜度
加起來即可

• 操作分塊

這個trick有意思，先掛題：CF342E Xenia and Tree
可以發(fā)現(xiàn)，對于加點操作與詢問操作，有兩種最基礎(chǔ)的做法，一種是直接跑遍歷，查詢復(fù)雜度 \(O(n)\) 修改復(fù)雜度 \(O(1)\)
第二種是預(yù)處理,加點后進(jìn)行全圖遍歷,為每個結(jié)點賦答案值,修改復(fù)雜度 $ O(n) $ , 查詢復(fù)雜度 $ O(1) $,有點根號分治的意思了
補(bǔ)充一下,樹上任意兩點的距離 \(dis_{u,v}\) 可以用公式:\(dis_{u,v}=deep_u+deep_v-2*deep_{LCA_{u,v}}\),查詢復(fù)雜度是\(O(log_n)\)級
那么就可以每 $ \sqrt{n} $ 次操作后重構(gòu)樹上點答案值復(fù)雜為 \(O(n\sqrt{n})\),對根號操作內(nèi)次的查詢只讓初值與根號前方的點比較復(fù)雜度\(O(n\sqrt{n} log_n)\)
總的復(fù)雜度就是\(O(nlog_n+n\sqrt{n}+n\sqrt{n}log_n)\),LCA預(yù)處理+做法1+做法2

• 根號分治,根號平衡

也是學(xué)過的玩意,掛個鏈接筆記吧Link

• 總結(jié)

感覺今天最重要的是復(fù)雜度的分析,當(dāng)一道題的復(fù)雜度分析對了,再暴力的寫法也會是是最正確的AC

2025/07/18

省流: 抄PPTing.
如常,樓下,stntn 后面忘了

• 博弈論入門&概念

簡單來說,就是在兩個人都不會犯錯誤的情況下,探索某一人是必輸/必贏

• 簡單&博弈

1 .Bash博弈
\(n\) 個石頭,\(A,B\)輪流拿\(k \in[1.m]\) 個石頭,拿到最后一塊石頭的是獲勝者
solution:當(dāng)n是m+1的倍數(shù)時，先手必敗
2 .

考慮當(dāng)集合不為空時先手必勝---把1拿了
3 .

題面：CF1874A Jellyfish and Game
考慮只會一直交換全局amx與全局min，稍微約束判斷即可
4 .

題面：CF1860C Game on Permutation
博弈論遞推,求最長上升子序列
5 .

題面：CF1749C Number Game
模擬，隨著i的變大，會有一些數(shù)自己出局，A一定選最大的，B一定盡早淘汰最小的
6. \(Nim\)游戲:異或和不為時先手必勝---自己百度去

• 博弈圖和狀態(tài)

將每個狀態(tài)視為結(jié)點,連邊建圖,一般是\(DAG\)(有向無環(huán)圖)
狀態(tài):必勝,必敗....看名字就可以了

• SG函數(shù)

笑,上次寫這個忘了保存,不然我就直接掛鏈接了(
當(dāng)當(dāng)前結(jié)點\(u\)沒有后繼結(jié)點(必敗狀態(tài)),\(SG_u=0\)
否則\(SG_u=mex( \in_{Son_u}SG_v)\)
說人話就是所有兒子\(SG\)值組成的集合里取\(mex\)
\(mex\)指集合中沒有出現(xiàn)的最小的非負(fù)整數(shù)
起點\(S\)的\(SG\)函數(shù)值\(SG_s\)就是這個游戲的\(SG函數(shù)值\)
組合游戲的\(SG\)函數(shù)值就是所有子游戲的\(SG\)函數(shù)值的異或和
P3185 [HNOI2007] 分裂游戲
后面忘了，寫珂朵莉去了（

2025/07/19

今天考試,考試總結(jié)見:一點總結(jié)（

2025/07/20~2025/07/27

放一周的假

2025/07/27~2025/08/17

中山集訓(xùn),內(nèi)部消息,不透露

2025/08/21

今天是貪心專題，首先看了看dottle佬的ppt
所謂貪心其實就是證明最重要

1. P8082 [COCI 2011/2012 #4] KEKS
   從前往后去刪除，保留剩余k位中最大的一個
   貪心正確性顯然
2. P8898 [USACO22DEC] Feeding the Cows B
   可以發(fā)現(xiàn)每頭牛吃的屮離他越遠(yuǎn)越好,那么記錄最右側(cè)的屮位置,當(dāng)需要更新的時候就從該點往后找最遠(yuǎn)的位置填,由于記錄的最右位置只加不減,最多遍歷\(O(n)\)次,可以通過該題,正確性顯然
3. P6243 [USACO06OPEN] The Milk Queue G
   this
   貪心式子可以用數(shù)學(xué)歸納法得出/證明
4. P2255 [USACO14JAN] Recording the Moolympics S
   考慮如果只有一個錄音機(jī)時怎么做:
   將所有活動結(jié)束時間排序,然后從初始結(jié)點開始能選就選
   兩個錄音機(jī)怎么做?
   將活動結(jié)束時間進(jìn)行排序,然后遍歷每個,用空閑的那個能選就選
5. P2945 [USACO09MAR] Sand Castle S
   考慮將a與b分別從高到低排序,然后直接每對算貢獻(xiàn)
6. P8896 「DPOI-1」道路規(guī)劃
   考慮拓?fù)?競賽圖的DAG,問題轉(zhuǎn)換成在序列上把其變成在[L,R]之間的數(shù)
7. CF525D Arthur and Walls
   貪心染色,dfs一個?點要被替換，當(dāng)且僅當(dāng)有一個包含它的2×2的矩陣中除它之外全是.點,向八個方向同時擴(kuò)展
8. CF3D Least Cost Bracket Sequence
   先把字符串中的問號都換成右括號，如果左括號比右括號多，則在前面所有原來問號上找左右差值最小的換掉
9. CF1208G Polygons
   考慮什么時候加入 \(k\) 邊形是最優(yōu)的?
   eg:如果我要加入6邊形,那么我一定會先加入3邊形,因為三邊型的頂點全部被六邊形覆蓋著
   可以推廣:如果我要加入 \(k\) 邊形,那么 \(k\) 邊形前所有與\(k\)有公因數(shù)的 \(p\) 邊形都會與 \(k\) 邊形有相同的交點
   所有每次添加 \(k\) 邊形時會增加在 \(k\) 前面與 \(k\) 互質(zhì)的數(shù)個數(shù)個新點
   也就是\(\phi(k)\) !
   然后就很顯然了,歐拉函數(shù)是積性函數(shù),當(dāng)\(gcd(a,b)=1\) 時 \(\phi(a*b)=\phi(a)*\phi(b)\),直接用篩法將質(zhì)數(shù)與歐拉數(shù)一起篩出即可
   最后將 3~n 的所有歐拉排序,選 k 個最小的,加上初始三角形的2即為答案

2025/08/22

貪官模擬器，今天接著貪

1. CF1085E Vasya and Templates
   考慮分討，但是我沒大懂，先跳過吧
2. P4765 [CERC2014] The Imp
   看到物品數(shù)量為 \(10^5\) 但最多只會有 \(k<=10\) 個物品被變成灰,考慮dp
   設(shè) \(dp_{i,j}\) 表示買到前 \(i\) 個物品時用了 \(j\) 次魔法的最大收益,很容易推出轉(zhuǎn)移方程:
   \(dp_{i,0}=max(dp_{i-1,0} , a[i].val-a[i].cost)\) 先手表示選與不選
   \(dp_{i,j}=max(dp_{i-1,j} , min(dp_{i-1,j-1}-a[i].cost,a[i].val-a[i].cost))\)
   max表示我的最優(yōu)狀態(tài),min表示惡魔干擾的最劣狀態(tài)
   轉(zhuǎn)移順序?價值從大到小!
   考慮如果從小到大去選,即使不使用魔法你也無法最大化收益,所以直接從大到小去選!
3. CF1685C Bring Balance
   考慮一個結(jié)論:任何括號數(shù)相同的括號序列在翻轉(zhuǎn)兩次以內(nèi)一定會完成匹配
   證明:
   將左括號看成+1,右括號看成-1,就發(fā)現(xiàn)原先的括號序列變成了一條折線圖,當(dāng)折線上到x軸以下(小于零)才是不正確的
   令\(a[i]\)為折線的前綴和數(shù)組,記錄x為最大值,翻轉(zhuǎn) \([1,x],[x,n*2]\) 一定可以獲得合法序列
   考慮怎么只翻轉(zhuǎn)一次:
   令 l,r 是最前和最后一個前綴和小于 0 的位置，那么最終翻轉(zhuǎn)的區(qū)間 \([L,R]\) 一定要滿足 \(L≤l,R>r\) 貪心地選擇 \(L≤l,R>r\) 且\(a_{L-1},a_R\)最大的 \([L,R]\) 檢驗即可
4. CF436E Cardboard Box
   記錄 \(i\) 關(guān)拿一顆星的代價為 \(a_i\) , 拿兩顆星的代價為 \(b_i\)
   考慮如何從有 \(i\) 顆星星推到第 \(i+1\) 顆星星,有四種情況:

• 新選一個獲取一顆星星的關(guān) \(i\) ,代價為 \(a_i\)
• 將一個原來只有一顆星的關(guān)卡`\(i\) 變成兩顆星 , 代價為 \(b_i-a_i\)
• 將一個原來只有一顆星的關(guān)卡 \(i\) 反悔一顆星 , 從新的關(guān)卡 \(j\) 拿兩顆星 , 代價為 \(b_j-a_i\)
• 將一個原來有兩顆星的關(guān)卡 \(i\) 反悔成只有一顆星 , 從新的關(guān)卡 \(j\) 拿兩顆星 , 代價為 \((a_i-b_i)+b_j\)
  那么我們維護(hù)五個優(yōu)先隊列,每次取隊首更新即可

5. CF1348F Phoenix and Memory
   懶得寫了:
   

2025/08/23

今天上午考試,第二道題懂了,沒切出來

1. A. 剪切字符串 (lcp)
   詐騙題,考慮答案上界,其實第一串選 \(n-2\),第二串選\(1\),第三串選\(1\)
   \(lcp(a,b)+lcp(a,c)+lcp(b,c)\)最長也只能是\(3\)
   當(dāng)?shù)诙c第一串有一個不同,那么答案上界就變成\(1\)了,當(dāng)?shù)谝淮诙谌加幸粋€不同,答案上界就是0了,分討即可
2. B. 深度優(yōu)先搜索樹（dfs）
   考慮什么時候可以有答案:當(dāng)返祖邊出現(xiàn)時,答案為\(2^k\),\(k\)是返祖邊的數(shù)量
3. C. 巡邏網(wǎng)絡(luò)（net）
   狀壓||隨機(jī)化,還沒調(diào)出來,因為最多只選四個點嘛
4. D. 彩色括號（witch)
   這個是真不會
5. 雜題P4679[ZJOI2011] 道館之戰(zhàn)
   惡心!調(diào)了3hours了,調(diào)不出來,整體上是樹剖+線段樹,不過要有維護(hù)信息有點多而已()

2025/08/24

晚上ABC,和明天混在一起總結(jié)

2025/08/25

貪貪貪,嘻嘻嘻

1. P1650 田忌賽馬
   考慮跑兩遍,第一遍統(tǒng)計可以獲勝的最大值,第二遍找平局
   將齊王和田忌的??按照從小到大排序,從小到大枚舉田忌的??,從大到小枚舉齊王的??,當(dāng)田忌的??比齊王的??快,貪心選擇
2. P5749 [IOI 2019] 排列鞋子
   考慮每次移動都是從右邊最近的一個過來,那么開n給vector,存每種鞋子的位置,從右往左,樹狀數(shù)組跳過中間的鞋子
3. P4823 [TJOI2013] 拯救小矮人
   按照逃生高度排序,貪心dp
4. P6927 [ICPC 2016 WF] Swap Space
   考慮分成兩個數(shù)組,第一個存 \(a<=b\) 的 第二個存 \(a>b\) 的,分別按a從小到大,b從大到小排序,最后模擬即可
   貪心正確性顯然
5. AT_agc023_f [AGC023F] 01 on Tree
   考慮貪心，對于所有權(quán)值為0的點，當(dāng)他的父節(jié)點全部拍下來了，那么把它馬上拍下來就是最優(yōu)的
   所以可以考慮將子節(jié)點和父節(jié)點合并，考慮如何維護(hù)合并后結(jié)點的權(quán)值？
   現(xiàn)在我有兩個個結(jié)點a，b，那么當(dāng)a放在前面時會產(chǎn)生\(a_{cnt1}*b_{cnt0}\)對逆序?qū)?\(cnt_{1/0}\)表示該節(jié)點下方權(quán)值為\(1/0\)的結(jié)點個數(shù),當(dāng)b放在前面時會產(chǎn)生\(b_{cnt1}*a_{cnt0}\)對逆序?qū)?br> 所以當(dāng)a比b更優(yōu)時,即產(chǎn)生的逆序?qū)ψ钌?有\(a_{cnt1}*b_{cnt0}<a_{cnt0}*b_{cnt1}\),即以此優(yōu)先隊列排序即可
   code:
6. 好消息,調(diào)出了道館之戰(zhàn)!

2025/08/26

最后的一天貪心了(

1. P4409 [ZJOI2006] 皇帝的煩惱
   每個勛章最多給\(n/2\)個將軍,那么可以得出式子\(ans=\dfrac{\sum_{i=1}^{n}a_i}{\lfloor\frac{n}{2}\rfloor}\)
   一共需要的勛章數(shù)/每種勛章最多可以給多少人
2. P2123 皇后游戲
   考慮怎么排律是最優(yōu)的
   
3. AT_arc076_b [ABC065D] Built?
   將x與y分別排序,給相鄰兩項分別連邊,最后跑最小生成樹即可,正確性顯然

2025/08/27

晚上神秘CF，明天補(bǔ)吧

2025/08/28

進(jìn)入了構(gòu)造板塊,首先觀摩了 \(dottle\) 佬的ppt,知道了一個神秘構(gòu)造稱呼:人類智慧

1. CF1512D Corrupted Array
   考慮什么時候可以由a變成b
   記錄一個最大值maxx,一個次大值se_max
   要么是a中所有數(shù)加起來等于se_max,maxx是隨機(jī)數(shù)
   要么其他數(shù)加起來等于maxx,用maxx-sum和等于的那個數(shù)是隨機(jī)數(shù),分討即可
2. AT_abc185_f [ABC185F] Range Xor Query
   為什么在構(gòu)造題單里???線段樹裸題哇(
3. P5595 【XR-4】歌唱比賽
   首先考慮什么時候無解:形如ZZZXY,就是Z只能出現(xiàn)在末尾一段連續(xù)段中
   然后做完了,X:0 9 Y:9 0 Z: 1 1
4. P3514 [POI 2011] LIZ-Lollipop
   考慮一個結(jié)論:當(dāng)X可以得到,那么X-2也可以得到
   證明:

• 當(dāng)x兩端都為1時,同時刪去兩邊,滿足x-2
• 當(dāng)x一端為二時,刪去該端,滿足x-2
  那么很顯然了,通過找到最大奇數(shù)與最大偶數(shù),然后\(1e6\)的范圍L,R桶處理即可

5. P3640 [APIO2013] 出題人
   造數(shù)據(jù)，不嘻嘻，考慮不同最短路算法的卡掉，分析算法結(jié)構(gòu)

2025/08/29

構(gòu)構(gòu)造造

1. AT_agc029_c [AGC029C] Lexicographic constraints
   考慮二分答案,如何check?
   模擬進(jìn)位即可,注意從大到小的答案為一的特判即可
2. AT_agc035_c [AGC035C] Skolem XOR Tree
   分奇偶討論,考慮兩種路徑

• x->x+1->1->x' (x%2==0)
• x->x-1->1->x' (x%2==1)

2025/08/30

考試，放假

2025/08/31

常規(guī)收假

2025/09/01

補(bǔ)了MZOJ的考試題與ABC的題，abc421f是唐題，鏈表思想，記錄next數(shù)組即可

2025/09/02

考慮雜題，四道題一下午只做出來兩道（

1. P3423 [POI 2005] BAN-Bank Notes
   完蛋了,先沒有看出來背包,然后看出來了不會寫,花了0.5h+重新學(xué)習(xí)01背包(
   首先多重背包求最小方案,采用二進(jìn)制優(yōu)化(其實就是拆位)
   然后考慮如何輸出方案,可以發(fā)現(xiàn),dp時記錄一下選擇,dfs就可以了
2. P4563 [JXOI2018] 守衛(wèi)
   你被騙了,不要像我一樣去搞斜率與凸包,\(O(n^3)\) 滾出(
   考慮每個區(qū)間 \([L,R]\) 一定會在 \(R\) 位置放一個人,那么我們以 \(R\) 為基礎(chǔ)(一定要選), \(O(n)\) 枚舉 \(L\)
   那么枚舉的復(fù)雜度為 \(O(n^2)\) , 考慮區(qū)間dp合出答案
   對于每個枚舉的 \(R\) ,在枚舉它的 \(L\) 時記錄一個可以看到的最左邊的端點 \(P\) 那么 \(P\) 之前的就一定是之前訪問過的區(qū)間,
   那么記區(qū)間 \([a,b]\) 的最小放人值為\(dp_{a,b}\) 則\(dp_{a,a}=1\)
   \(dp_{L,R}=dp_{L,P}+1 , dp_{P,R}=1\)
   最后異或上所有的 \(dp\) 值即為答案

2025/09/04

同上面02,四,二,懂?
考慮雜題，四道題一下午只做出來一道（

1. P5504 [JSOI2011] 檸檬
   斜率優(yōu)化版子,李超樹輪椅,嘻嘻嘻
2. P3209 [HNOI2010] 平面圖判定
   考慮每一條邊要么在曼哈頓回路形成的?內(nèi),要么在?外,2-Sat做完了,考慮平面圖的歐拉公式: \(v+p-e=2\)

2025/09/05

考慮考試（炸

2025/09/06

考慮vp abc，abc422e 隨機(jī)化有點意思，時間復(fù)雜度之王（

2025/09/09

考慮vp cf 1048 Div2

1. CF2139A Maple and Multiplication
   非常簡單，考慮每次變化三種情況：

• a==b (0次)
• gcd(a,b)a||gcd(a,b)b (1次)
• gcd(a,b)==1 (2次)

2. CF2139B Cake Collection
   非常煎蛋，你考慮貪心去取，排序后按最后一秒從大到小分配求和即可
3. CF2138A Cake Assignment
   肥腸煎蛋，你觀察到變換的次數(shù)不超過120次，且每次變換的上一步是固定的，所以你倒著去搜一遍即可
4. CF2138B Antiamuny Wants to Learn Swap
   你注意到值域范圍很小，然后轉(zhuǎn)化一下題意，你就是去求區(qū)間有沒有逆序三元組，線段覆蓋區(qū)間查最小值，三顆線段樹維護(hù)最近前驅(qū)即可
5. 不會了（

2025/09/12

考慮vp cf 1049 Div2

1. CF2140A Shift Sort
   考慮位移的實質(zhì)：交換兩個數(shù),那么兩個指針前后掃，貪心匹配即可
2. CF2140B Another Divisibility Problem
   注意到每次拼接的x都可以是原數(shù)的二倍，然后你把原數(shù)乘二。輸出來就行了）
3. CF2140C Ultimate Value
   不難發(fā)現(xiàn)，Bob總會在第二輪選擇結(jié)束游戲（Alice可以一直還原Bob的行動，然后只會增加權(quán)值）
   那么Alice肯定會在第一輪完成最優(yōu)解

• +_min 換 -_max
• +_l 換 +_r
  判斷即可

4. CF2140D A Cruel Segment's Thesis
   訪問 題解 謝謝喵）

2025/09/13

考慮上午核桃OJ考試下午四道雜題，下午忙于補(bǔ)做題記錄只寫了一道雜題（

1. P3177 [HAOI2015] 樹上染色
   比較裸的樹形dp，轉(zhuǎn)移方程為
   \(dp[u][j+p]= \max\limits_{v\in Son_u}^{j \le Siz_u p\le Siz_v}dp[u][j]+dp[v][p]+val*w\)

其中 dp[u][m] 表示以u為根的字樹里選m個點染色對答案的貢獻(xiàn)，從下往上dfs時處理合并，枚舉j，p算貢獻(xiàn)
其中w為連邊的權(quán)值，val 為經(jīng)過的次數(shù) 復(fù)雜度為\(O(n^2)\)

2025/09/16

考慮寫CF2144喵

1. CF2144A Cut the Array
   n <100 直接枚舉即可
2. CF2144B Maximum Cost Permutation
   貪心從前往后和從后往前找即可
3. CF2144C Non-Descending Arrays
   訪問 題解 謝謝喵

2025/09/26

前面幾天都在vp喵，補(bǔ)題不想記喵

1. P2709 小B的詢問
   莫隊版子喵，奇奇偶偶排排序序。
2. P12621 [ICPC 2025 NAC] Circle of Leaf
   考慮樹形dp，\(dp_{u,0/1}\) 表示以 u 為根的子樹中方案，從下往上推
3. P4198 樓房重建
   使用線段樹維護(hù)一段最長上升的斜率， \(O( \log n)\) 來 \(push\) 下放

2025/10/03

考慮今天的考試）

• A. 大數(shù)定理（largenumber)
  所有可能的兩個數(shù)一定是相距 \((n-1)/2\) 才能只刪這兩個數(shù)達(dá)到序列為1的，單調(diào)棧模擬即可

2025/10/04

記一下今天vp的cf

1. A. Increase or Smash
   你發(fā)現(xiàn)n很小,于是可以while來砸碎序列中除零以外的最小值
   當(dāng)序列中全部為0,結(jié)束并輸出
2. B. Catching the Krug
   考慮取橫縱坐標(biāo)的差的絕對值,因為B可以斜著走,所以A左右橫跳是沒有用的.
   A只能往相反方向逃竄,加上A反與B距離判斷max即可
3. C. Triple Removal
   由于只有0/1所以數(shù)量要么是三元組個數(shù)+1,要么是三元組的個數(shù)
   前綴和判斷是否有00或者11即可
4. D. Division Versus Addition
   訪問題解謝謝喵）
5. P5278 算術(shù)天才⑨與等差數(shù)列
   考慮形成等差序列的三個限制條件，設(shè)判斷區(qū)間l，r是否可以形成公差為k的等差序列

• \([l,r].max-[l,r].min=(r-l)*k\)
• \([l,r]所有相鄰差值的gcd=k\)
• \([l,r]沒有相同的數(shù)\)
  一二條維護(hù)區(qū)間最大最小值，區(qū)間差值gcd即可

2025/10/10

記一下今天的雜題)今天的題比較好

1. P2964 [USACO09NOV] A Coin Game S
   看到這題,第一眼就可以搜索dp定義
   \(dp[i][j]\)表示取到第i個限制為j個時的最優(yōu)解
   \(dp[i][j]= \max_{x \in_{}[1,j]}(\sum_{a_i}-dp[i+x][x*2] )\)
   就這樣去搜,開\(O_2\)就可以A了,
   但是你發(fā)現(xiàn)記搜的復(fù)雜度實際上有\(O(n^3)\)
   所以正解不是直接搜
   你發(fā)現(xiàn)其實dp[i][j]與dp[i][j-1]狀態(tài)數(shù)只有兩項差距,所以可以直接特判
2. P1758 [NOI2009] 管道取珠
   ddddpppp
   考慮組合意義（
   你發(fā)現(xiàn)一下：
   我們要求 \(\sum a_i^2\)
   我們獨(dú)立地進(jìn)行兩次游戲，每次游戲都用相同的初始管道狀態(tài)（相同的 s1 和 s2）
   那么兩場游戲都產(chǎn)生第i種序列的方案數(shù)？
   第一次有\(a_i\)種方案產(chǎn)生序列\(i\)
   第二次有\(a_i\)種方案產(chǎn)生序列\(i\)
   兩次都產(chǎn)生序列\(a_i\)的方案數(shù)就是\(a_i \times a_i=a_i^2\)
   所以實際上跑一邊計數(shù)dp即可
   因為兩個游戲完全對稱，并且要求輸出序列相同，實際上我們可以用一個四維 DP 來解：
   定義 dp[i][j][x][y] 表示：
   第一個游戲已取出了 i 個上管道球和 j 個下管道球（即剩余 n-i 上球, m-j 下球）
   第二個游戲已取出了 x 個上管道球和 y 個下管道球（即剩余 n-x 上球, m-y 下球）
   此時兩個游戲已產(chǎn)生的輸出序列完全相同（即之前取出的球顏色序列一樣）
   的方案數(shù)。
   最終答案： dp[n][m][n][m]（兩個游戲都取完，輸出序列相同）
   然后你發(fā)現(xiàn)i+j=x+y只有取得球數(shù)量相等,序列才可能相同,所以可以優(yōu)化掉一維
   
   然后你可以發(fā)現(xiàn)f[i][j][k]只與上一個狀態(tài)有關(guān),考慮作滾動即可
   
3. P2943 [USACO09MAR] Cleaning Up G
   維護(hù)pre顏色段dp即可

2025/10/11

記一下今天的考試題)

1. A. 瘟疫（plague）
   你發(fā)現(xiàn)一下，n，m的范圍只有兩千，那么你bfs遍歷一遍圖，把連通塊標(biāo)上vis，記下大小
   然后再掃一遍遍歷四個編號，取min即可
2. B. 顫骨圖騰（beacon)
   你發(fā)現(xiàn)你記錄一下pre和net，然后每次就可以 \(n/k\) 遍歷
   然后對每個k記錄一下，做完了？
   $ \frac{1}{n}+\frac{2}{n}+\frac{3}{n}+\cdots+\frac{n-2}{n}+\frac{n-1}{n}+\frac{n}{n} $
   時間很熟悉啊，你就是調(diào)和級數(shù)喵！
   原式$ \approx n \log n $]
3. C. 死靈法師（wizard）
   神秘東西,不會(
4. D. 亡靈騎士（rider）
   你考慮背包+剪枝
   首先直接作 \(o(r^2)\) 的背包一定是不行的你肯定要優(yōu)化
   還有剪枝，考慮什么時候卡的最慢：
   

其中 \(x=sqrt(n)\)

2025/10/12

記一下昨天的abc

1. C題
   讀了題，k<=10
   狀壓一下，枚舉做完了
2. D題
   k<=10
   爆搜遍歷一遍，然后記憶化一下，做完了
3. E題
   不會（
4. F題
   折半搜索，直接枚舉
   考慮長度為n的不相鄰序列只與長度為(n-1),(n-2)的不相鄰序列有關(guān)，斐波拉契數(shù)列，其中\(fib_{30}\)大概是832040，然后記一下有沒有選第一個，選作后一個，然后二分查一下，拼一拼就做完了）

2025/10/14

記一下今天的 cf1057 的vp

1. CF2153A Circle of Apple Trees
   簽到題，派一遍序然后跑一遍就做完了
2. CF2153B Bitwise Reversion
   被騙了（
   你考慮一下:

$ \because $

• $ a \And b = x$
• $ a \And c = y$
• $ b \And c = z$

$ \therefore $

好了，三個疊一起，判斷一下是否相等即可（

3. CF2153C Symmetrical Polygons
   考慮首先一定要把成對的取完，然后成對的和加上一個數(shù)大于另一個數(shù)，二分判斷即可
4. CF2153D Not Alone
   隔位dp，你發(fā)現(xiàn)要么兩個相鄰，要么三個相鄰，因為所有數(shù)都可以被二和三完全分解，所以dp時只需要考慮前三位，關(guān)于斷環(huán)成鏈，只需要右移三次dp判斷即可
   

2025/10/17

今天補(bǔ)了CF1058vp

記一下一道不錯的圖論：

• AT_joisc2016_j 危険なスケート
  你考慮到相鄰格子最多走兩步，滑行到終點處只需要一步，建邊跑最短路！

2025/10/18

敲了洛谷下午的SCP-S組模擬賽

2025/10/19

vp了abc428,記錄一下

1. A - Grandma's Footsteps
   模擬即可
2. B - Most Frequent Substrings
   string 排序即可
3. C - Brackets Stack Query
   括號匹配,考慮維護(hù)折線,滿足值為0且前方?jīng)]有負(fù)數(shù)位置才可判斷Yes
4. D - 183184
   你發(fā)現(xiàn)你可以把新加x后組成的數(shù)表示為 \(c\times 10^i+x\)
   用上界開根號減去下界即可,枚舉這個 \(i\) 并且累加答案即可
5. Farthest Vertex
   發(fā)現(xiàn)所有取值只會在直徑的兩端之一,兩遍 dfs 找到編號最大直徑端點,搜出直徑上的所有點并記錄答案
   再往下搜出答案處理即可

2025/10/20

vp了CF1060
完成了斜率優(yōu)化的施工:Link
完成了對拍教程的施工:Link

2025/10/21

考了試,發(fā)現(xiàn)\(n^2\) 過了1e5,嘻嘻
完成了樹上拓?fù)湫蛴嫈?shù)的施工,在神秘題單里

2025/10/22

記一下今天的ARC208

1. A - Bitwise OR Game
   首先你想到普通\(Nim\)游戲的結(jié)論：
   \(Nim\)游戲中，狀態(tài)($a_1,a_2,\cdots,a_n $)是必敗狀態(tài)當(dāng)且僅當(dāng) \(a_{1} \oplus a_{2} \oplus \cdots \oplus a_{n}=0\)
   你\(Nim\)游戲是最后一個取不到東西的人輸
   本題保證了區(qū)間或值相同，那么每一位都要留一個1
   相當(dāng)于先把每一位扣掉一個1再進(jìn)行\(Nim\)游戲

2. B - Sum of Mod
   考慮什么構(gòu)造是最優(yōu)的
   \(a\to 2a-1\)
   二分起點構(gòu)造即可

3. C - Mod of XOR
   分討

2025/10/23

1. tree
   你發(fā)現(xiàn)選的點與之前的無關(guān)，每個點選了后一定會產(chǎn)生兒子數(shù)量的連通塊，所以直接背包即可

2. perm
   考慮兩個序列的轉(zhuǎn)化：
   你選一個數(shù) x
   把\(\le x\)的數(shù)全部賦成0，其他的賦成1
   那么對于原來的序列，就會變成一個01串
   我們用01串來探索兩個串能不能轉(zhuǎn)移得到
   那么就會有結(jié)論：
   轉(zhuǎn)移后的串一定會在每個1都在轉(zhuǎn)移前的串右邊
   因為每次是在交換逆序?qū)Γ钥梢宰约和埔幌拢辛诉@個結(jié)論再來考慮dp
   dp考慮狀壓，\(n\le 20\)所以可以直接記那些值用過了，從1~n枚舉，每次把序列中新加入的數(shù)置成1，記現(xiàn)在的序列為s
   那么在枚舉當(dāng)前的狀態(tài)，s1的數(shù)量要與枚舉的串1的數(shù)量相等（預(yù)處理局面對應(yīng)的1的數(shù)量，\(o(1)\)）
   然后設(shè)枚舉的串為t，\(s \to t\)要合法時，t就是合法串了，對于合法串，我們枚舉其所有1的位置，走到該局面的方案數(shù)就是將枚舉的1視為最后一個添加的局面的方案數(shù)，使用lowbit維護(hù)即可

3. P10641 BZOJ3252 攻略
   首先你考慮將其轉(zhuǎn)化成選k條不交的樹鏈
   樹剖中對重兒子的定義是siz最大的，其實也可以維護(hù)到底部權(quán)職最大的
   考慮樹剖中有多少兒子就有多少鏈
   那么對所有鏈取鏈頂，以向下最大權(quán)值為val，提出來排序選前k個即可

4. P3313 [SDOI2014] 旅行
   你考慮樹剖后開顏色數(shù)課線段樹
   動態(tài)開點，支刪點操作即可

5. P4114 Qtree1
   樹剖版子

6. P3674 小清新人渣的本愿
   首先離線莫隊，這個非常顯然
   如何維護(hù)兩個數(shù)的差為x？
   其實就是問你區(qū)間\([l,r]\)中有沒有 \(n\) 和 \(n+x\)
   那么開一個 bitset s 為值域桶，將 bitset 向左移動 x 位，得到一個和原來偏移量 \(+x\) 的桶
   將原先的桶和現(xiàn)在的桶與起來，若有重合，就會有 1，使用 any()函數(shù) 判斷即可
   如何維護(hù)兩個數(shù)的和為x?
   考慮區(qū)間 \([l,r]\) 中有沒有一些東西
   考慮記 \(x=m+n\) 那么有一個神奇的轉(zhuǎn)化：
   記大常數(shù) \(C\) ，記錄值域范圍中 x 的 \(C-x\)
   再維護(hù)一個 bitset t 維護(hù) \(C-x\)
   你發(fā)現(xiàn) \((C-m)-(C-n)=n-m\)
   將 t 右移 \(C-x\)位
   那么 t 中的數(shù)就會變成 \(C-n-(C-x)\) = \(x-n\)
   那么我們只需要在 s 中查詢有沒有 \(x-n\) 即可，因為 n 是一定有的，與起來判斷
   如何維護(hù)兩個數(shù)的積為x？
   直接 \(O(sqrt(x))\) 枚舉x的因數(shù)，\(O(1)\)判斷即可，時間復(fù)雜度為 \(O(m\times \sqrt{x})\)

2025/10/24

咦！1024程序員節(jié)！

1. P10639 BZOJ4695 最佳女選手
   吉司機(jī)線段樹版子，考慮勢能分析復(fù)雜度，發(fā)現(xiàn)記錄了區(qū)間次小值與區(qū)間次大值，所以在懶標(biāo)記下放時有延遲，是\(O(n \log ^2n)\)的東西
2. AT_abc134_f [ABC134F] Permutation Oddness
   非常神秘的dp題，你發(fā)現(xiàn)可以將其抽象其球和盒子配對
   -
   是一個非常像二分圖匹配的東西
   然后你對這個東西dp，每條連邊的貢獻(xiàn)是經(jīng)過的黑線數(shù)量對這個詭異的東西做dp即可（
3. P7828 [CCO 2021] Swap Swap Sort
   首先讀懂題：給你一個排序權(quán)重和一個初始序列，每次交換相鄰兩個權(quán)重，問此時有多少逆序?qū)?br> 你發(fā)現(xiàn)每次只交換相鄰兩個數(shù)的權(quán)重，我們記兩個數(shù) \(x,y\) 的\(x\) 在 \(y\) 前面的數(shù)量為 \((x,y)\)
   那么每次的交換可以看成的\(lastans+(x,y)-(y,x)\)
   你發(fā)現(xiàn) 逆序?qū)?順序?qū)?總對數(shù) 即記值 \(x\) 出現(xiàn)為\(cnt_x\)
   $\therefore cnt_x \times cnt_y=(x,y)+(y,x) $
   而記下出現(xiàn)次數(shù)是可以 \(O(1)\) 維護(hù)的
   所以我們可以把式子轉(zhuǎn)化:

• 所以瓶頸在于維護(hù)\((y,x)\)
  發(fā)現(xiàn)值域很小所以考慮對數(shù)字\(x\)的出現(xiàn)次數(shù)\(cnt_x\)進(jìn)行根號分治
  我們設(shè)閾值為 \(S\)
  當(dāng) \(cnt_x\) 小于 \(S\) 時我們記一個 \(vector\) 存 \(x\) 出現(xiàn)的每一個下標(biāo)，兩個都小于 \(S\) 時直接用雙指針掃一遍 ， 這么做是 \(O(q \times S)\) 的，因為出現(xiàn)次數(shù)不超過 \(S\) 嘛
  當(dāng) \(cnt_x\) 大于 \(S\) 時，我們直接枚舉后預(yù)處理出來對每種顏色的貢獻(xiàn)，那么這種復(fù)雜度是 \(O(n\times \frac{n}{S})\)
  這么做的總復(fù)雜度是\(O(q \times S+n\times \frac{n}{S})\)
  問題在于 \(S\) 的取值, 均值不等式
  \(\sqrt{a*b}\le \frac{a+b}{2}\) 當(dāng) \(a=b\) 時取等，即\(q\times S=n \times \frac{n}{S}\)

• 所以理論當(dāng)\(S\)取100時取得最優(yōu)復(fù)雜度，實測有波動
  還有就是對最開始還要求一遍初始逆序?qū)Γ矣玫臋?quán)值線段樹）

4. AT_abc295_h [ABC295Ex] E or m
   記一下輪廓線dp的思想，輪廓線dp，也叫按位dp，指只記錄一層有效狀態(tài)，向下dp比如在種草問題中，不中相鄰的草，那么我們就通過上一層的狀態(tài)來之轉(zhuǎn)移合法狀態(tài)，不用枚舉了

2025/10/25

記一道Ynoi

• P5048 [Ynoi2019 模擬賽] Yuno loves sqrt technology III
  強(qiáng)制在線區(qū)間眾數(shù)，考慮分塊
  記\(f[i][j]\)表示塊 \(i\) 到塊 \(j\) 的區(qū)間眾數(shù)最大值
  對于每個值用一個\(vector\)記下下標(biāo)，暴力遍歷散塊，那么記一下這個位置在 vector 里的下標(biāo)，l塊就向右推 res 個，看下標(biāo)是否在r的范圍內(nèi)，r塊就左推 res 個，看下標(biāo)是否在l的范圍內(nèi)，如果成立，res++即可
  神秘三倍經(jīng)驗）

2025/10/26

記一下今天的 abc 429
d. 訪問 題解謝謝喵
e. 多元bfs，搜索即可

1. CF1422D Returning Home
   你發(fā)現(xiàn)n很大，瞬移點很少，那么可以直接建邊瞬移點，考慮最短路，很明顯的是按照x,y排序，相鄰兩個點才建邊，記得加上起點，在遍歷一遍所以點到終點的曼哈頓距離+dis的最小值即可
2. P5906 【模板】回滾莫隊&不刪除莫隊
   考慮回滾莫隊的思想，你發(fā)現(xiàn)刪除操作非常困難，因為你不好維護(hù)次大值，次次大值，次次次大值，那么我們就不要刪除了，對于所以左端點在同一塊內(nèi)的詢問分為一組，對于每一組詢問，將右端點升序排列，那么每次莫隊從左往右掃，只后不前，左端點每次暴力遍歷，每跑到一個右端點就丟掉左端點，讓左端點回歸R[ql]+1,至于在同一塊內(nèi)的，直接暴力做！

2025/10/27

考試，跳過了

2025/10/28

vp了CF，不想記

2025/10/29

1. A. 乘法(mul)
   你發(fā)現(xiàn)這是一個很類似二進(jìn)制加減法東西
   那么有一個結(jié)論：
   單個的一直接加上這一位，消耗為二
   兩個及以上的一可以通過二進(jìn)制減法消耗為四
   然后考慮只隔一個零的情況：
   你發(fā)現(xiàn)要是隔了一個0也是二進(jìn)制減法一起做，然后會有消耗二
2. B. 環(huán)(circle)
   你發(fā)現(xiàn)這是一個類似于分層圖的東西，對于\(u_0\to v_1,u_1\to v_2,u_2\to v_0\)
   然后只要可以從\(u_0\to u_1\)這個點即成立，寫個tarjan判斷強(qiáng)連通分量即可
3. C. 柵欄(fence)
   數(shù)據(jù)結(jié)構(gòu)題，加上一點點貪心
   首先先把最大高度序列維護(hù)出來
   做一個類似滑動窗口的東西，區(qū)間查一下最小值，在開一顆線段樹更新一下區(qū)間最大值
   然后你會發(fā)現(xiàn)對于一段確定的最高的最大高度序列，相鄰不一樣的一定會讓操作次數(shù)+1
   而相鄰相同的就是長度除x向上取整即可

2025/10/30

考慮記一下最近欠補(bǔ)的題

1. P3472 [POI 2008] MAF-Mafia
   首先，可以對斃人來建出一棵樹，首先很明顯，那些沒人打的角色是肯定不會死的，所以他們打的人都是必死的，你發(fā)現(xiàn)在對于一條鏈，有必死的，有必活的，有不確定的
   

• 于是拓?fù)渑芤槐椋钌倬褪歉粢粋€殺一個，用這個可死可不死玩意數(shù)量/2.最大就是從后往前打，全殺了
  但是還要考慮環(huán)狀結(jié)構(gòu)
  
• 一樣的，最小死一半，最大剩一個，注意判斷自環(huán)即可

2. P13984 數(shù)列分塊入門 9
   發(fā)現(xiàn)可以離線，顯然可以回滾Mo隊，只增不減，區(qū)間更新，記得離散化
3. P1337 [JSOI2004] 平衡點 / 吊打XXX
   Mo擬退火，對于每個點直接在其基礎(chǔ)上加上隨機(jī)值，概率替換答案，平衡態(tài)勢能最小
   完成了Mo擬退火的維修Link
4. AT_abc273_g [ABC273G] Row Column Sums 2
   考慮dp求解。
   \(dp_{i,j,k,l}\)表示還剩下 i 個 1 類行和 j 個 2 類行，來滿足 k 個 1 類列和 l 個 2 類列的方案數(shù)。
   然后你會發(fā)現(xiàn)\(i+2\times j=k+2\times l\)
   枚舉第一維，根據(jù)等式優(yōu)化掉一維
   
5. AT_abc303_g [ABC303G] Bags Game
   考慮區(qū)間dp \(d_{i,j}\) 表示區(qū)間[i,j]可以獲得的最大收益，由于n是300，區(qū)間dp套ds優(yōu)化找最小值即可
6. AT_abc138_f [ABC138F] Coincidence
   數(shù)位dp
   考慮 :
   $2x\le y $ , \(y \% x < y-x\)
   $y<2x $ , \(y \% x=y-x\)
   \(y-x\le y^x\)
   那么只有 \(y<2x\) 才會有合法答案
   又是 \(y>x\) 所以合法 x，y位數(shù)相同
   當(dāng)y二進(jìn)制位為1，x可以是0可以是1
   當(dāng)y二進(jìn)制位為0，x該位只能是0
7. AT_abc225_f [ABC225F] String Cards
   結(jié)論題，排序a+b<b+a后dp即可
8. CF620F Xors on Segments
   偷了，前綴和暴力 \(n^2\) 可以過嘻嘻
9. CF442D Adam and Tree
   記錄f數(shù)組為節(jié)點子樹最大顏色數(shù)
   記錄重，次重兒子，每次暴力向上更新至無法影響上層答案，類似樹剖的復(fù)雜度，不超過\(\log\)
10. P5500 [LnOI2019] 真正的 OIer 從不女裝
    你發(fā)現(xiàn)再怎么翻轉(zhuǎn)序列，也無法組成新的連續(xù)段，最多讓首位接起來，所以其實只用維護(hù)每一塊的左右顏色與最長顏色段即可
    使用線段樹維護(hù)，但是現(xiàn)在還沒有調(diào)出來

2025/10/31

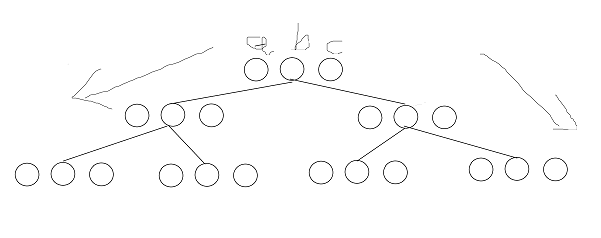
1. P1852 跳跳棋
   考慮兩個狀態(tài)之間的關(guān)系
   首先對于一個狀態(tài)的轉(zhuǎn)移
   
   這是非常顯然的，由于只能跳過一個棋子
   所以說中間的那兩個只會執(zhí)行一個
   你會發(fā)現(xiàn)只有左右會往外擴(kuò)張，只有中間那個是收縮的
   猜想一下，所有狀態(tài)是會匯聚到一個點上的，也就是不能在收縮的，也就是會在\(b-a=c-b\)的時候收縮到極致
   那么以這個點為根節(jié)點，可以拓展出一個類似于樹結(jié)構(gòu)的東西
   
   為什么兩個點的收縮點是唯一確定的？
   假設(shè)
   \(x , x+a , x+a+a\) 可以擴(kuò)展到 \(z+qc,z+tc,q+pc\)
   \(y , y+b , y+b+b\) 也可以擴(kuò)展到 \(z+qc,q+tc,q+pc\)
   那么已知每次擴(kuò)展后的坐標(biāo)都是 \(m+qn\) 的形式出現(xiàn)，所以\(x=y=z,a=b=c\)
   那么每個狀態(tài)對應(yīng)的收縮節(jié)點就是唯一的
   那么先找到初始三元組的收縮三元組和目標(biāo)三元組的收縮三元組，只有相同才可以YES
   但是你發(fā)現(xiàn)值域是\(1e^9\)的
   所以直接轉(zhuǎn)移肯定是不行的，考慮如何加速轉(zhuǎn)移
   發(fā)現(xiàn)三個跳棋是沒有區(qū)別的，那么每次跳躍可以看作\(a\to a+ab,b\to b+ab\)直接跳就可以了
   所以具體來說，跳躍是\(O(\log_n)\)的
   在把目標(biāo)和當(dāng)前的提到同一深度后二分找\(LCA\)即可

2025/11/01

下午是S組復(fù)賽，上午看了最短路的版子，并查集的版子，柯樹模擬退火，結(jié)果只用上了并查集

1. P14361 [CSP-S 2025] 社團(tuán)招新 / club
   首先你發(fā)現(xiàn)個社團(tuán)最多有$ \frac{n}{2} $ 個人
   那么比較顯然的，每個人要么選最大值要么選次大值，不會考慮最小值
   那么你考慮對于一個人，選他的最大值和次大值的差異在哪里
   如果選了最大值，那么對于這個人就是最優(yōu)的，如果選了次大值，相較于選最大值，虧了最大值減次大值的代價
   那我們要和最大，就要虧的最少，考慮當(dāng)一個玩意滿了就每次把它代價最小的丟出去，把代價大的攥在手里
   按照代價排序丟點即可
2. P14362 [CSP-S 2025] 道路修復(fù) / road（民間數(shù)據(jù)）
   你先跑一遍最小生成樹，把邊的條數(shù)優(yōu)化到，n
   再對所有村莊作dfs式的狀壓最小生成樹，是對的（

2025/11/02

開一下今天abc的 c，d，e

1. C - Truck Driver
   從后往前掃一遍，將后面第A個a的位置和第B個b的位置預(yù)處理出來
   答案就是每個點的合法B位置減A位置的和
2. D - Neighbor Distance
   對這個東西開一個set，開map存最近的點位置，二分找到位置后比較大小更新，最后insert做完了
3. E - Shift String
   kmp版子，動態(tài)加一下就可以了

2025/11/03

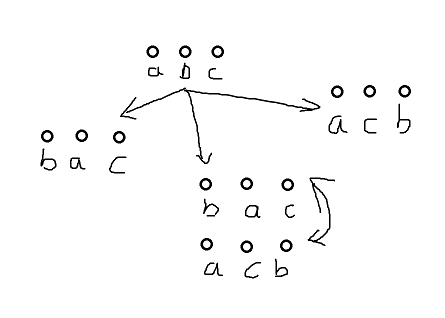
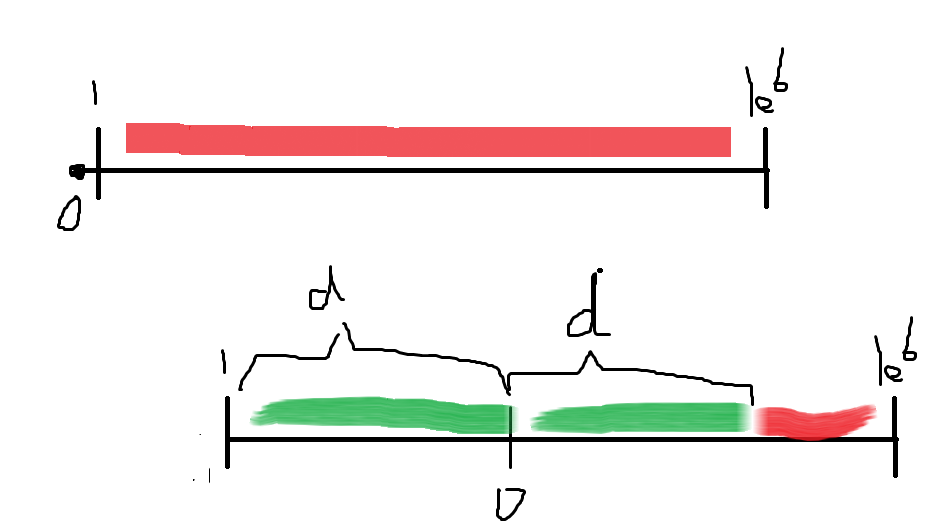
1. AT_arc149_d [ARC149D] Simultaneous Sugoroku
   首先明確，我們移動的是原點，這樣維護(hù)每個點的相對位置
   然后對于第一次原點移動后，可以發(fā)現(xiàn)將\([1,1e^6]\)的區(qū)間分成了兩個部分
   
   如圖所示，綠色的區(qū)間可以作映射！
   把小區(qū)間映射到大區(qū)間，YES時答案相等，NO時答案互為相反數(shù)
   就這樣映射后縮短左右區(qū)間大小查值答案時類似記搜一遍
   只有最后作搜索，是線性的！

2025/11/04

1. A. 矩陣matrix
   可以發(fā)現(xiàn)，這是一個保證有解的東西
   那么考慮它的解到底是什么樣子的
   類似于
   \(\begin{align*} 01010\\ 00000 \\ 10101 \\ 00000 \\ 10101 \end{align*}\)
   一定要隔一列，一行
   還要考慮豎線的情況
   就是把這個玩意翻轉(zhuǎn)一下，做完了
2. B. 介值intermediate
   首先有一個結(jié)論：一段合法子序列最多只有四種顏色
   把這個東西拍到序列上，用值域表示
   
   就是這個樣子的
   那么先考了\((km)^2\)枚舉直接計數(shù)
   會超時間，那么考慮對區(qū)間固定計數(shù)
   
   其實會有累加計數(shù)！
   將前綴記下累加右移即可
   還要考慮用兩個值累計，以達(dá)到去重的效果