考慮一下 splay 的復(fù)雜度分析。

當(dāng)需要遞歸的子樹較大時(shí)，rotate 操作可以使勢(shì)能降低。
反之勢(shì)能會(huì)上升，但是次數(shù)不會(huì)超過 \(O(\log n)\)。
那么，當(dāng)需要遞歸的子樹較小的時(shí)候?yàn)槭裁床恢苯舆f歸呢？

算法描述

當(dāng)我們需要插入一個(gè)數(shù)字 \(x\)，當(dāng)前節(jié)點(diǎn)為 \(a\) 時(shí)，進(jìn)行以下操作：

1. 若子節(jié)點(diǎn)為空，直接結(jié)束。
2. 若走一步之后為空，直接結(jié)束。
3. 若可以向下走兩步（還未找到插入位置）且兩步之后的子樹大小 < \(k\) 倍當(dāng)前子樹大小，則直接遞歸兩步。
4. 否則，若兩步方向相同，則進(jìn)行一次 zig 操作，否則進(jìn)行 zig-zag 操作。

其中 \(k\) 為常數(shù)，zig 與 zig-zag 操作的定義與 splay 相同。

為了便于理解，代碼貼在這里。

int insert(int a, int b)
{
	if (!a)
		return newnode(b);
	while (true)
	{
		int x = (b >= tree[a].val), y = tree[a].son[x];
		if (!y)
		{
			tree[a].son[x] = newnode(b);
			break;
		}
		int c = (b >= tree[y].val);
		if (tree[tree[y].son[c]].siz < tree[a].siz * eps)
		{
			tree[y].son[c] = insert(tree[y].son[c], b);
			update(y); break;
		}
		if (c != x)
			tree[a].son[x] = rotate(y, c);
		a = rotate(a, x);
	}
	update(a);
	return a;
}

后面我們將證明：每次旋轉(zhuǎn)必定使勢(shì)能降低 \(O(1)\)，每次插入至多增加 \(O(1)\) 勢(shì)能。

復(fù)雜度

我們定義勢(shì)能 \(E = \sum \limits_{u} \log size(u)\)。

\(1, 2, 3\) 操作自不必多說，不影響勢(shì)能，且至多進(jìn)行 \(O(\log n)\) 次（每次使得當(dāng)前子樹大小縮小 \(k\) 倍）。

首先我們考慮 zig 操作的復(fù)雜度。

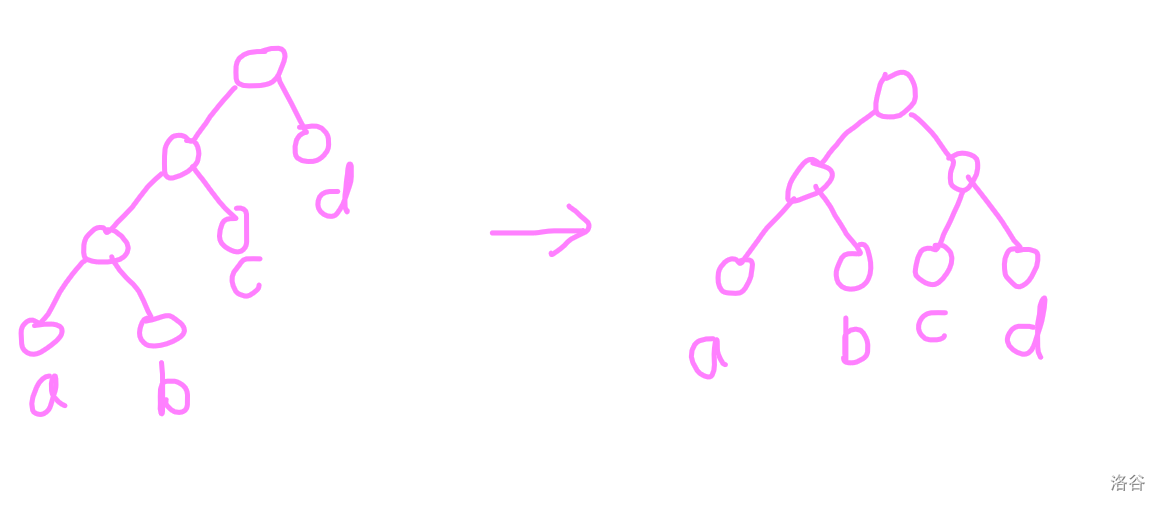
其中 \(k = \frac{a+b}{a+b+c+d}\)。
即證：\(\log(a+b+c) - \log(c+d) > 1\)。

我們只需要保證 \(a+b > 2(c+d)\) 即可。
因此 \(k > \frac{2}{3}\) 即可滿足條件。

然后我們考慮 zig-zag 操作的復(fù)雜度。

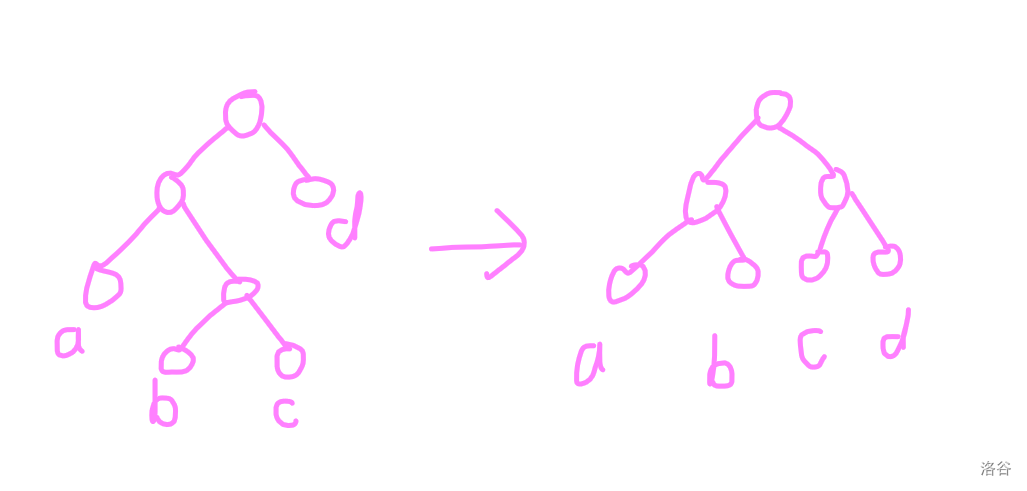
其中 \(k = \frac{b+c}{a+b+c+d}\)。
即證：\(\log(a+b+c)+\log(b+c)-\log(a+b)-\log(c+d) > 1\)。

這里 \(b\) 與 \(c\) 等價(jià)，因此我們欽定 \(b > c\)。

如果我們可以保證 \(\frac{1}{2}b^2 > 2ad\) 與 \(\frac{1}{2}b^2 > 2bd\) 均成立就可以了。

如果我們保證 \(b+c>8(a+d)\)，由于 \(b>c\)，所以 \(b>4(a+d)\)，滿足條件。
因此 \(k>\frac{8}{9}\) 時(shí)這部分成立。

因此只需要 \(b>2(a+d)\) 即可保證這部分成立，得到 \(k > \frac{4}{5}\)。

綜上所述，取 \(k > \frac{8}{9}\) 可以保證 4 操作的復(fù)雜度。

（事實(shí)上我們可以將這個(gè)界降低到 \(\frac{\sqrt{13}+3}{\sqrt{13}+5} \approx 0.77\)）

或許可以更低，但是畢竟是不影響復(fù)雜度的。
（Warning：實(shí)現(xiàn)時(shí)這個(gè)常數(shù)取的更低能換取更優(yōu)秀的常數(shù)，但是可能會(huì)導(dǎo)致復(fù)雜度錯(cuò)誤）

最后是插入導(dǎo)致的勢(shì)能增加量。
考慮只有 \(1, 2, 3\) 操作導(dǎo)致當(dāng)前深度增加，且插入后自下而上第 \(k\) 層的子樹大小不小于 \(O(exp(k))\)。
那么勢(shì)能增加量 \(\sum \limits _{k = 1} ^{\log n} \log (\exp(k)+1) - \log ( \exp(k)) \sim O(1)\)。

綜上，遞歸操作單次不超過 \(O(\log n)\)，旋轉(zhuǎn)操作均攤 \(O(n)\)。

Bonus

由于勢(shì)能函數(shù)定義與 splay 完全相同，所以可以繼續(xù)使用 splay 的全部操作。
相較于常規(guī)的 splay，這種實(shí)現(xiàn)方式無(wú)法將需要訪問的點(diǎn)旋轉(zhuǎn)到根（只能保證旋轉(zhuǎn)之后深度 \(O(\log n)\)）。
但是換來了其它的性質(zhì)（常數(shù)更小，理論不需要遞歸，不需要棧，不需要記錄父節(jié)點(diǎn)，勢(shì)能增加量更低）。
提交記錄，用時(shí) 6.3s
由于前驅(qū)后繼操作不方便實(shí)現(xiàn)，為了偷懶 使用了 \(kth(rank(x) - 1)\) 來實(shí)現(xiàn)。

平衡性

結(jié)束了嗎？

如果只有上述操作，我們來看一看這個(gè)東西是否平衡。

若一個(gè)節(jié)點(diǎn) \(u\) 的兩個(gè)子節(jié)點(diǎn) \(a, b\) 滿足 \(\frac{1}{16} size(a) \le size(b) \le 16size(a)\)，則稱 \(u\) 為平衡的。
若 \(\frac{1}{17} size(a) < size(b) < \frac{1}{16} size(a)\) 或 \(a, b\) 互換，則稱 \(u\) 是失衡的。

接下來我們要證明：任意時(shí)刻一條鏈上不會(huì)出現(xiàn)三個(gè)相鄰的失衡點(diǎn)。

先考慮插入的過程。
考慮鏈上三個(gè)節(jié)點(diǎn) \(a, b, c\)，其中 \(a, c\) 的深度為偶數(shù)。
則我們有 \(size(c) < \frac{8}{9} size(a)\)。
若加點(diǎn)之后 \(a, b\) 均為失衡點(diǎn)，則有 \(size(c) > \frac{17^2}{18^2} size(a)\)，顯然不成立。
因此 \(a, b\) 中至少存在一個(gè)平衡點(diǎn)。
所以插入后的祖先鏈上不會(huì)出現(xiàn)三個(gè)相鄰的失衡點(diǎn)。

然后考慮旋轉(zhuǎn)的過程。

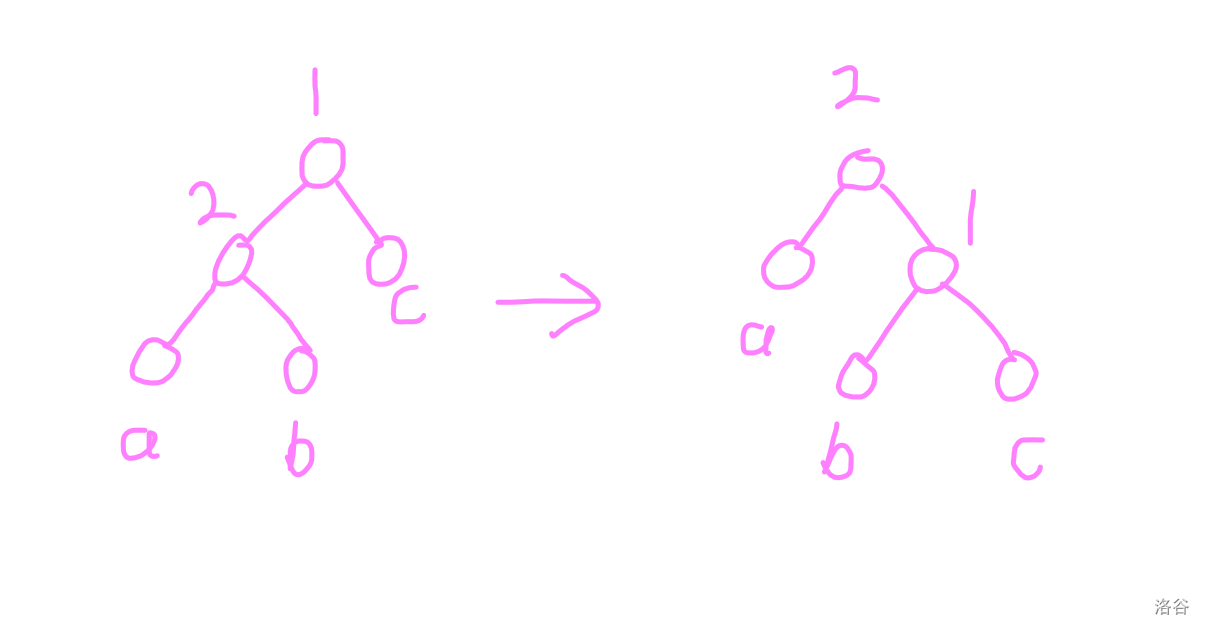
這里已知 \(a > 8(b+c)\)。

首先考慮 \(2\) 節(jié)點(diǎn)什么時(shí)候會(huì)失衡。
由于 \(a > b + c\)，所以只能是 \(b+c < \frac{1}{16} a\)。
若旋轉(zhuǎn)前 \(1, 2\) 中存在平衡點(diǎn)，則 \(b+c > \frac{1}{16} a\)，不成立。
若旋轉(zhuǎn)前 \(1, 2\) 均為失衡點(diǎn)，則 \(b > \frac{1}{17} a\)，\(c > \frac{1}{17} (a + b)\)。
所以有 \(b+c > \frac{2}{17} a + \frac{1}{17^2} a > \frac{1}{16} a\)。
因此 \(2\) 節(jié)點(diǎn)旋轉(zhuǎn)后必定平衡。

然后考慮 \(1\) 節(jié)點(diǎn)什么時(shí)候失衡。
由于 \(c > \frac{1}{17} (a+b) > \frac{1}{17}(9b + 8c) > \frac{9}{17}b\)，所以只可能是 \(c > b\) 導(dǎo)致的失衡。
由于 \(c < \frac{1}{8} a\)，\(b > \frac{1}{17} a\)，所以有 \(b > \frac{8}{17} c\)。

綜上，旋轉(zhuǎn)之后 \(1, 2\) 一定都平衡。

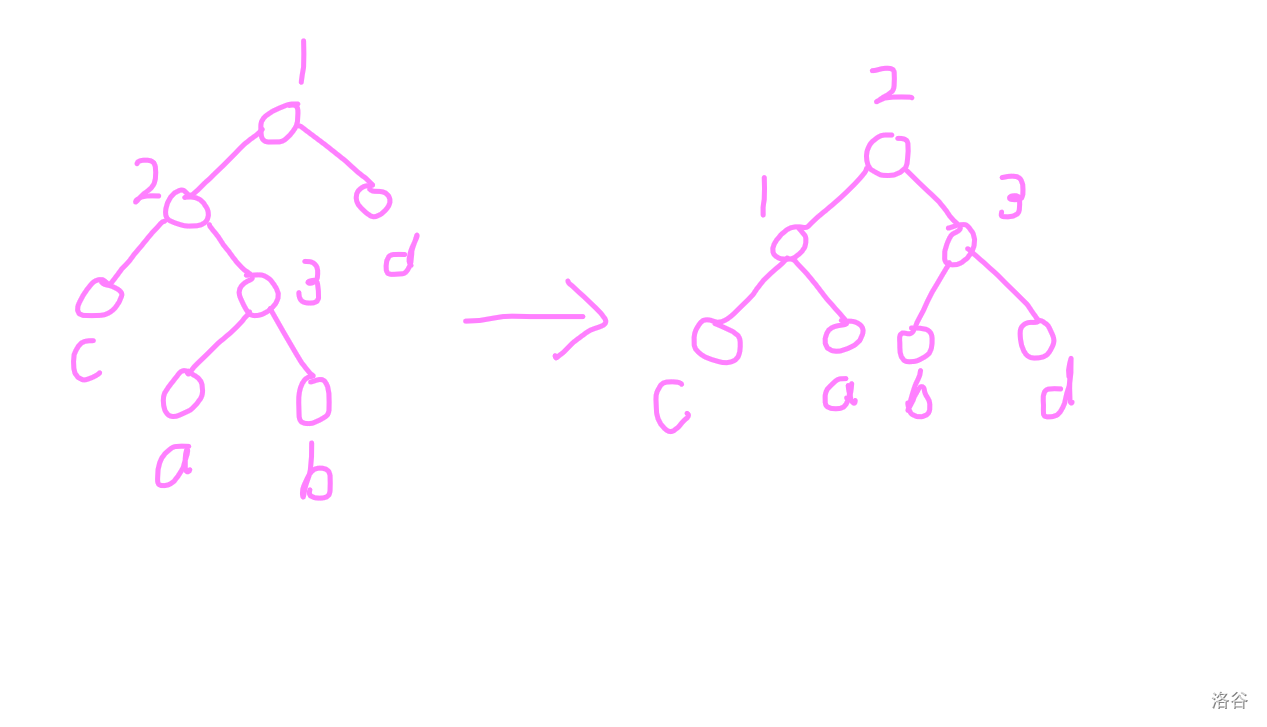
這里已知 \(a + b > 8(c + d)\)。

首先考慮 \(3\) 節(jié)點(diǎn)是否會(huì)失衡。
考慮旋轉(zhuǎn)前 \(1, 2, 3\) 中至多出現(xiàn)兩個(gè)失衡點(diǎn)，因此 \(d > \frac{18}{16 \times 17} b > \frac{1}{16} b\)，\(3\) 節(jié)點(diǎn)不會(huì)失衡。
然后考慮 \(2\) 節(jié)點(diǎn)。
我們有 \(d > \frac{1}{18} (a+b+c+d)\)，\(b > \frac{1}{18} (a+b) > \frac{8}{9 \times 18} (a+b+c+d)\)。
因此

我們又有 \(c > \frac{1}{17}(a+b)\)，\(a > \frac{1}{18} (a+b)\)。
因此

綜上，\(2\) 節(jié)點(diǎn)旋轉(zhuǎn)后必定平衡。

最后是 \(1\) 節(jié)點(diǎn)。
若旋轉(zhuǎn)前 \(2, 3\) 存在平衡節(jié)點(diǎn)，則 \(c > \frac{1}{16} a\)，旋轉(zhuǎn)后平衡。
若 \(2, 3\) 均失衡，則旋前 \(a, c\) 的父節(jié)點(diǎn)均失衡，旋后仍然失衡，不影響性質(zhì)。

綜上，進(jìn)行旋轉(zhuǎn)操作后仍能保持性質(zhì)。

這樣，我們就成功證明了這棵樹重量平衡。

刪除

Q：那么該如何刪除節(jié)點(diǎn)呢？

這里我們使用經(jīng)典做法：和右子樹的后繼節(jié)點(diǎn)交換然后刪除后繼。

首先，如果沿用勢(shì)能分析的話，我們發(fā)現(xiàn)直接刪即可。
畢竟勢(shì)能是不增的。

但刪除會(huì)導(dǎo)致失衡節(jié)點(diǎn)增加，影響我們的平衡性分析。
這可能會(huì)導(dǎo)致單次操作復(fù)雜度變高（因此查詢也必須加入平衡維護(hù)）
因此我們需要在刪除時(shí)加入維護(hù)平衡的操作。

大致來說，就是在遞歸過程中如果出現(xiàn)臨近失衡的節(jié)點(diǎn)（刪除后失衡），則反方向旋轉(zhuǎn)。

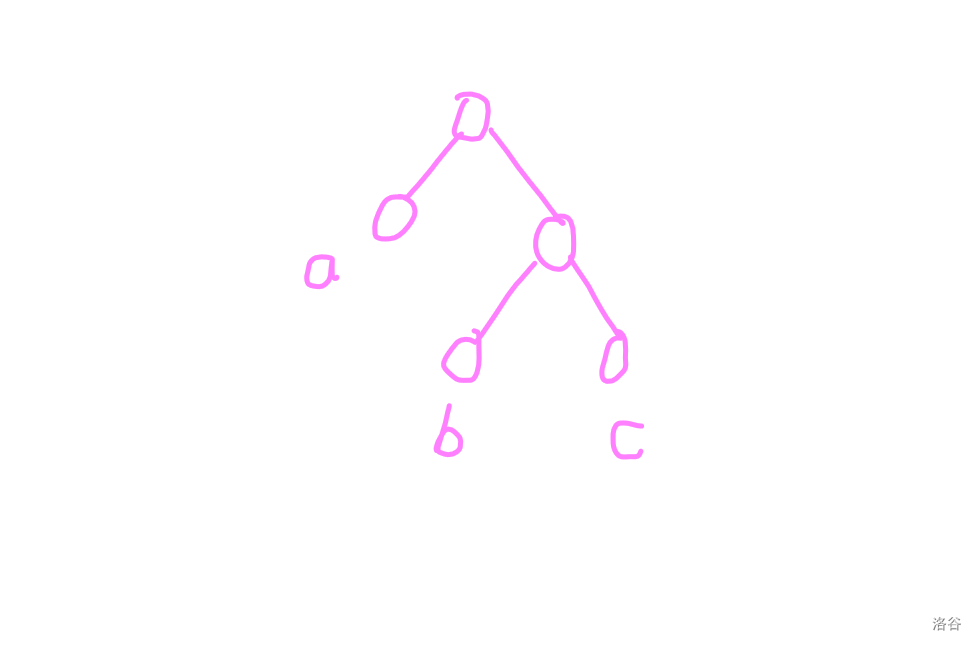
設(shè)我們要遞歸的節(jié)點(diǎn)為 \(a\)，且 \(a < \frac{1}{16} (b+c)\)。

1. 若 \(b > 7(a+c)\)，則進(jìn)行 zig-zag 操作。
2. 否則進(jìn)行一次 zig 操作。

（Warning：這里將 \(b > 7(a+c)\) 改為 \(b > 8(a+c)\) 會(huì)導(dǎo)致證不出來）

勢(shì)能分析就免了。
我們直接證明其平衡即可。

這里我們有 \(b < \frac{7}{8}(a+b+c)\)，\(c < \frac{1}{17}(a+b+c)\)，因此 \(a > \frac{1}{16} (a+b+c)\)，先保證 \(2\) 節(jié)點(diǎn)性質(zhì)不被破壞。
我們還有 \(b > \frac{1}{17} a\)，\(c > \frac{1}{17} a\)，所以 \(b+c > \frac{1}{9} a\)，即可保證 \(2\) 節(jié)點(diǎn)不臨近失衡。

熟悉嗎？
首先我們有 \(b+d > (\frac{1}{18} + \frac{7}{8 \times 18})(a+b+c+d) > \frac{1}{10}(a+c)\)，則 \(2\) 節(jié)點(diǎn)不會(huì)臨近失衡。
剩余的的平衡性分析可以直接沿用前面的，因?yàn)椴⒉恍枰?\(a + b > 8(c + d)\) 這個(gè)條件。

綜上，旋轉(zhuǎn)操作可以使當(dāng)前節(jié)點(diǎn)擺脫臨近失衡狀態(tài)且不影響整棵樹的平衡性質(zhì)。

結(jié)算

既然如此，就只需要在插入、刪除的時(shí)候進(jìn)行旋轉(zhuǎn)操作。
由于任意時(shí)刻平衡，所以查詢時(shí)直接遍歷即可，不需要進(jìn)行平衡維護(hù)。

洛谷板子（\(10^6\)）：
提交記錄，5.7s
5.48s，去掉了 update 并優(yōu)化了邏輯

Loj 板子（\(10^5\)）：
ofast 加持 53ms