你好呀，我是歪歪。

前幾天在網上沖浪的時候看到一個消息，關于智能密碼鎖的。

就是這種玩意：

當時我看到的那個消息說，開密碼鎖的時候，你輸入的數字串只要包含你真正的密碼就能開鎖。

比如，假設你的密碼是：250818。

那你在按密碼的時候輸入“123250818456”也能開鎖。

怎么可能是這樣的開鎖邏輯呢，密碼都沒匹配上，門就開了，這不扯呢嗎？

所以，我當時以為拍視頻的人在一本正經的搞抽象呢，

直到有天晚上回家，在電梯里我突然又想起了這個段子。

于是想著驗證一下。

嘿，你猜怎么著？

我開鎖的時候在正確的密碼前后故意多輸入了幾個數字，然后再按“#”，門開了。

還真不是段子。

當時我大概是這樣的：

這玩意有點意思啊。

一般來說我都是用指紋解鎖，但是有時候晚上出去跑步，回來之后手上都是汗，指紋識別老是失敗。

這種情況下，我就會選擇輸入密碼。

而我之前輸入密碼偶爾按快了，會出現按錯一位的情況。

這個時候我就會輕輕的嘆一口氣，表示無奈，然后先輸入一個“#”，讓電子鎖喊一聲“密碼錯誤”，再重新輸入。

那天我驗證了“在按#之前只要包含正確密碼輸入，門就能打開的這個邏輯”之后，顯得我之前的一些操作像是個傻子。

同時我也興奮的把 Max 同學叫來，給她分享了我的偉大發(fā)現。

她說：這不會是 BUG 吧？

我作為程序員，就聽不得 BUG 這個東西。

于是我又淺淺的研究了一下，發(fā)現這玩意，還真是 feature，不是 BUG。

“這不是 BUG，這是 feature”，沒想到這句話還真會出現在一些非狡辯的場景下。

甚至這個 feature 幾乎是密碼鎖的標配，而這個功能還有個專門的名稱叫：虛位密碼。

我在購物網站上隨便找一個密碼鎖，都有相關的介紹：

看介紹，這個功能的使用場景主要就是當有人在你旁邊，你又不方便讓他回避的時候，你就可以在真實的密碼前面輸入一些干擾項，輸入的長一點，也不怕別有用心的人偷窺了。

這個功能怎么說呢？

我個人認為是聊勝于無，因為我沒有這個場景。

但是如果你告訴我，在輸密碼的時候，自己純純手滑，輸錯了，不用按“#”，讓密碼鎖喊一聲“密碼錯誤”，而是可以直接重新輸入一遍。

那我覺得這個功能是真好用。

因為這個場景是我真有。

問題就來了

我在了解到這個現象之后，自然而然的就帶入了程序員思維。

所以，那么問題就來了。

假設，現在這是一個面試的場景，面試官要求你寫一個邏輯來實現上面“虛位算法”的邏輯：

//判斷sourceStr中是否有targetStr
public static boolean checkStr(String sourceStr,String targetStr) {}

你會怎么搞？

首先我們來分析一下。

假設我的密碼是：250818。

要判斷我輸入的一串數字中是否也有 250818 這個序列存在，首先可以確定的是，我們要拿到這兩個輸入串，然后按照字符，逐個對比。

也就是要把 sourceStr、targetStr 轉化為 char[]，然后在 for 循環(huán)中逐一對比每個字符是否能對上。

而且因為有兩個數組，所以這個 for 循環(huán)還得是雙重 for 循環(huán)。

外層循環(huán)的是什么？

因為我們是要在 sourceStr，也就是用戶輸入的密碼里面找正確的密碼，所以外層循環(huán)的肯定得是 sourceStr。

拿著輸入密碼的第一個字符和 targetStr，也就是正確密碼的字符串對應的整個數組進行逐一比較，如果匹配上了，再拿輸入密碼的后續(xù)字符和正確密碼進行對比，循環(huán)往復，直到對比成功，或者整個輸入串對比完成。

這就對應著第二層循環(huán)的邏輯。

大體思路還是非常清晰的，但是我們還要解決一個問題：外層 for 循環(huán)的次數是多少次？

假設下面這個 for 循環(huán)就是在循環(huán) sourceStr，也就是我們要知道這里的 max 值應該是多少？

for (int i = 0; i <= max; i++) {}

這里我們做個假設：

sourceStr=123250818456
targetStr=2501818

那么我們外層的循環(huán)，從 sourceStr 的第一個字符“1”開始，最多循環(huán)到哪里的時候就能知道密碼是否能匹配上了？

是不是循環(huán)到123250【8】18456，這個【8】的時候？

因為算上這個【8】后面就只剩下 6 位長度了，如果這個 【8】 都還沒匹配上，那它后面的長度已經小于 6 位長度，再去匹配已經沒有意義了。

而這個“6 位長度”怎么來的？

是不是就是 targetStr 的長度？

所以 max 的值就是 sourceStr.length-targetStr.length。

按照上面的思路，完整的代碼就是長這樣的：

public static boolean checkStr(String sourceStr,String targetStr) {
    char[] source = sourceStr.toCharArray();
    char[] target = targetStr.toCharArray();
    int sourceCount = sourceStr.length();
    int targetCount = targetStr.length();
    char first = target[0]; // 目標串首字符
    int max = sourceCount - targetCount; // 最大可匹配起始位置

    // 2. 外層循環(huán)：遍歷源字符串
    for (int i = 0; i <= max; i++) {
        // 2.1 快速跳過不匹配位置
        if (source[i] != first) {
            while (++i <= max && source[i] != first); // 持續(xù)跳過直到找到首字符匹配
        }

        // 2.2 首字符匹配后，校驗后續(xù)字符
        if (i <= max) {
            int j = i + 1; // 源字符串下一個位置
            int end = j + targetCount - 1; // 目標串結束位置
            int k = 1; // 目標串下一個位置，在下面的for循環(huán)中進行遞增
            // 內層循環(huán)：逐字符比對
            for (; j < end && source[j] == target[k]; j++, k++);

            // 3. 校驗是否完全匹配
            if (j == end) {
                return true; // 返回匹配起始索引
            }
        }
    }
    return false; // 未找到
}

看到這里可能有小伙伴心理早就開始嘀咕了：整這么復雜干啥玩意？

我一行代碼就能秒了這題啊：

sourceStr.contains(targetStr);

好，不錯，很有精神！

那我問你：contains 的底層邏輯是怎么樣的？

啥，你說你不知道？

那你現在知道了，因為前面的實現邏輯，就是 Java 中 String 類 contains 方法的源碼：

contains 方法最終會調用到這個 indexOf 方法：

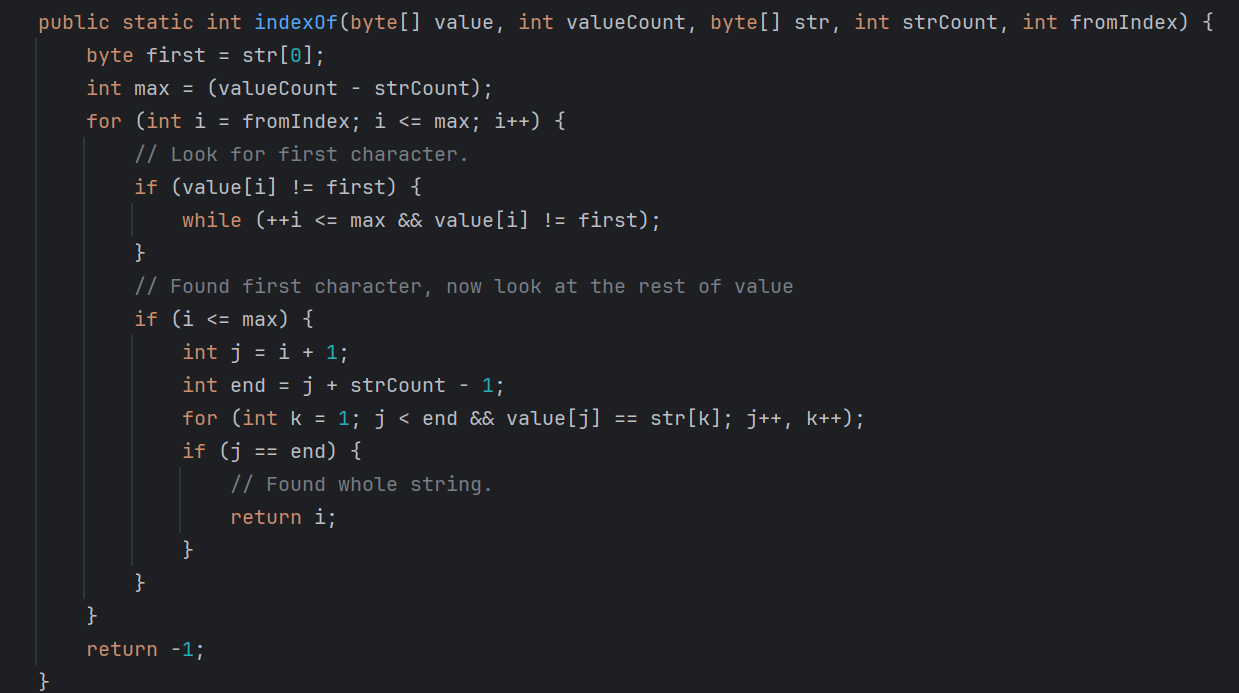
看了前面的邏輯，你再看這個 indexOf 方法你就會覺得：有點眼熟。

所以這個問題的關鍵，就是你要抓住關鍵的問題。

如果是在面試，你就答上面這個按照字符逐個對比的，然后補一句：這個思路和 contains 方法是一樣的。

如果是實際寫代碼，你一句話都不用說，contains 一把梭直接收工就完事。

這玩意就像面試的問你：手撕個 LFU 算法（最近最少使用算法） 來看看。

你回答的時候不能說“可以利用 LinkedHashMap 來實現”，對不對？

面試中，你得從 Node 開始撕，拿出雙向鏈表+哈希表的方案來。

至于實際寫代碼嘛...

對不起，我一個寫業(yè)務 的 Javaer，用不上這么高級的東西。

還有一個問題

其實在寫文章的時候，我突然還想到了一個問題。

一個非常致命的問題。

如果密碼鎖的“虛位密碼”這個邏輯真的成立，說明了什么？

說明密碼鎖的密碼是明文存儲的啊。

正常來說，密碼肯定是要加密存儲的，那不管你用什么加密方式。

250818 和 123250818456 加密出來的密文肯定是完全不一樣，天差地別的。

加密后，sourceStr.contains(targetStr) 的邏輯就完全不成立了啊。

所以，從這個現象來看，支持“虛位密碼”的密碼鎖的密碼可能是明文存儲的。

看到“明文存儲”這幾個字，是不是感覺很可怕？

如果來一次信息泄露，那不就變成“我家大門常打開”了嗎？

關于這個點，我是這樣想的。

密碼鎖的密碼并不會存儲在商家的服務器里面，而且存儲在密碼鎖的本地。

其實一般來說，明文存在本地也是有風險的，但是在密碼鎖的這個場景下，其實也是能接受的。

你想想，別人為了拿到你的明文密碼，是不是得把鎖拆下來搞搞逆向工程啥的。

那鎖都拆下來了，門不是輕輕一推就開了嗎，還要啥密碼？

One More Thing

我第一次得知密碼鎖的這個 feature ，并在自己家的密碼鎖上驗證過后，確實大為震驚。

震驚的點在于，我日常生活中每天都在用的東西居然還有隱藏功能。

這讓我莫名其妙的想到了另外一個點。

這個點是關于微信的。

微信，你點擊這個“拍攝”，有時候拍出來的照片質感很差：

因為調用的不是手機的原相機。

但是，如果你是安卓手機，那長按“相冊”按鈕大概 3 到 5 秒，就會喚醒手機的原相機。

當我第一次用上面的方式喚醒手機的原相機的時候，內心活動大概也是這樣的：

如果你不知道的話，你可以試一試。