數(shù)據(jù)結(jié)構(gòu)基礎(chǔ)溫故-5.圖（下）：最短路徑

圖的最重要的應(yīng)用之一就是在交通運(yùn)輸和通信網(wǎng)絡(luò)中尋找最短路徑。例如在交通網(wǎng)絡(luò)中經(jīng)常會(huì)遇到這樣的問(wèn)題：兩地之間是否有公路可通；在有多條公路可通的情況下，哪一條路徑是最短的等等。這就是帶權(quán)圖中求最短路徑的問(wèn)題，此時(shí)路徑的長(zhǎng)度不再是路徑上邊的數(shù)目總和，而是路徑上的邊所帶權(quán)值的和。

圖的最重要的應(yīng)用之一就是在交通運(yùn)輸和通信網(wǎng)絡(luò)中尋找最短路徑。例如在交通網(wǎng)絡(luò)中經(jīng)常會(huì)遇到這樣的問(wèn)題：兩地之間是否有公路可通；在有多條公路可通的情況下，哪一條路徑是最短的等等。這就是帶權(quán)圖中求最短路徑的問(wèn)題，此時(shí)路徑的長(zhǎng)度不再是路徑上邊的數(shù)目總和，而是路徑上的邊所帶權(quán)值的和。帶權(quán)圖分為無(wú)向帶權(quán)圖和有向帶權(quán)圖，但如果從A地到B地有一條公路，A地和B地的海拔高度不同，由于上坡和下坡的車速不同，那么邊<A,B>和邊<B,A>上表示行駛時(shí)間的權(quán)值也不同。考慮到交通網(wǎng)絡(luò)中的這種有向性，本篇也只討論有向帶權(quán)圖的最短路徑。一般習(xí)慣將路徑的開(kāi)始頂點(diǎn)成為源點(diǎn)，路徑的最后一個(gè)頂點(diǎn)成為終點(diǎn)。

一、單源點(diǎn)最短路徑

　　單源點(diǎn)最短路徑是指給定一個(gè)出發(fā)點(diǎn)（源點(diǎn)）和一個(gè)有向圖，求出源點(diǎn)到其他各頂點(diǎn)之間的最短路徑。對(duì)于下圖左邊所示的有向圖G，設(shè)頂點(diǎn)0為源點(diǎn)，則其到其他各頂點(diǎn)的最短路徑如下圖右邊所示。

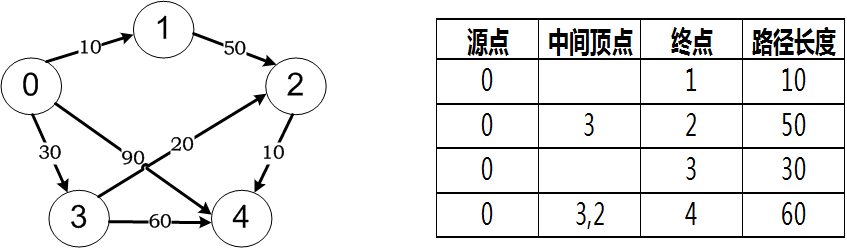
　　從上圖中可以看出，從源點(diǎn)0到終點(diǎn)4一共有4條路徑：

　　（1）0→4　　　　　　路徑長(zhǎng)度：90

　　（2）0→3→4　　　　路徑長(zhǎng)度：90

　　（3）0→1→2→4　　路徑長(zhǎng)度：70

　　（4）0→3→2→4　　路徑長(zhǎng)度：60

　　可以看出，源點(diǎn)0到終點(diǎn)4的最短路徑為第（4）條路徑。為了求出最短路徑，前人們已經(jīng)做很多工作，為我們奉獻(xiàn)了兩個(gè)重要的算法：Dijkstra（迪杰斯特拉）和Floyd（弗洛伊德）算法，下面我們就來(lái)看看這兩個(gè)算法。

二、Dijkstra算法

2.1 算法思想

　　Dijkstra在對(duì)最短路徑的求解方式做了大量的觀察之后，首先提出了按路徑長(zhǎng)度遞增產(chǎn)生與頂點(diǎn)之間的路徑最短的算法，以他的名字稱之為Dijkstra算法。

Dijkstra算法的基本思想是：將圖中頂點(diǎn)的集合分為兩組S和U，并按最短路徑長(zhǎng)度的遞增次序依次將集合U中的頂點(diǎn)加入到S中，在加入的過(guò)程中，總保持從原點(diǎn)v到S中各頂點(diǎn)的最短路徑長(zhǎng)度不大于從原點(diǎn)v到U中任何頂點(diǎn)的最短路徑長(zhǎng)度。

　　Dijkstra算法采用鄰接矩陣存儲(chǔ)圖的信息并計(jì)算源點(diǎn)到圖中其余頂點(diǎn)的最短路徑，如下圖所示。

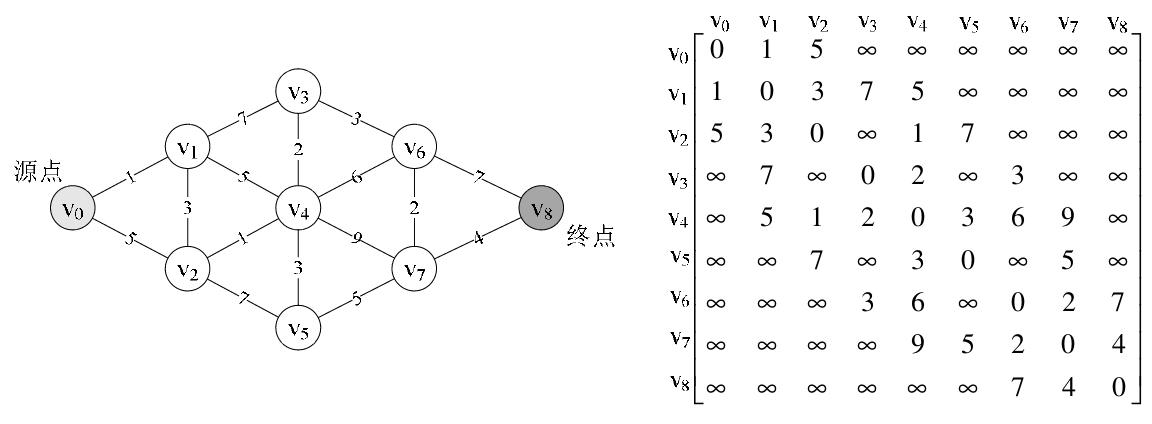
2.2 算法實(shí)現(xiàn)

　　（1）代碼實(shí)現(xiàn)

        static void Dijkstra(int[,] cost, int v)
        {
            int n = cost.GetLength(1); // 計(jì)算頂點(diǎn)個(gè)數(shù)
            int[] s = new int[n];      // 集合S
            int[] dist = new int[n];   // 結(jié)果集
            int[] path = new int[n];   // 路徑集

            for (int i = 0; i < n; i++)
            {
                // 初始化結(jié)果集
                dist[i] = cost[v, i];
                // 初始化路徑集
                if (cost[v, i] > 0)
                {
                    // 如果源點(diǎn)與頂點(diǎn)存在邊
                    path[i] = v;
                }
                else
                {
                    // 如果源點(diǎn)與頂點(diǎn)不存在邊
                    path[i] = -1;
                }
            }

            s[v] = 1;   // 將源點(diǎn)加入集合S
            path[v] = 0;

            for (int i = 0; i < n; i++)
            {
                int u = 0;  // 指示剩余頂點(diǎn)在dist集合中的最小值的索引號(hào)
                int minDis = int.MaxValue; // 指示剩余頂點(diǎn)在dist集合中的最小值大小

                // 01.計(jì)算dist集合中的最小值
                for (int j = 0; j < n; j++)
                {
                    if (s[j] == 0 && dist[j] > 0 && dist[j] < minDis)
                    {
                        u = j;
                        minDis = dist[j];
                    }
                }

                s[u] = 1; // 將抽出的頂點(diǎn)放入集合S中

                // 02.計(jì)算源點(diǎn)經(jīng)過(guò)頂點(diǎn)u到其余頂點(diǎn)的距離
                for (int j = 0; j < n; j++)
                {
                    // 如果頂點(diǎn)不在集合S中
                    if (s[j] == 0)
                    {
                        // 加入的頂點(diǎn)如與其余頂點(diǎn)存在邊，并且重新計(jì)算的值小于原值
                        if (cost[u, j] > 0 && (dist[j] == 0 || dist[u] + cost[u, j] < dist[j]))
                        {
                            // 計(jì)算更小的值代替原值
                            dist[j] = dist[u] + cost[u, j];
                            path[j] = u;
                        }
                    }
                }
            }


            // 打印源點(diǎn)到各頂點(diǎn)的路徑及距離
            for (int i = 0; i < n; i++)
            {
                if (s[i] == 1)
                {
                    Console.Write("從{0}到{1}的最短路徑為：", v, i);
                    Console.Write(v + "→");
                    // 使用遞歸獲取指定頂點(diǎn)在路徑上的前一頂點(diǎn)
                    GetPath(path, i, v);
                    Console.Write(i + Environment.NewLine + "SUM:");
                    Console.WriteLine("路徑長(zhǎng)度為：{0}", dist[i]);
                }
            }
        }

        static void GetPath(int[] path, int i, int v)
        {
            int k = path[i];
            if (k == v)
            {
                return;
            }

            GetPath(path, k, v);
            Console.Write(k + "→");
        }

　　這里經(jīng)歷了三個(gè)步驟，第一步是構(gòu)造集合U，第二步是尋找最短路徑，第三步是重新計(jì)算替換原有路徑。

　　（2）基本測(cè)試

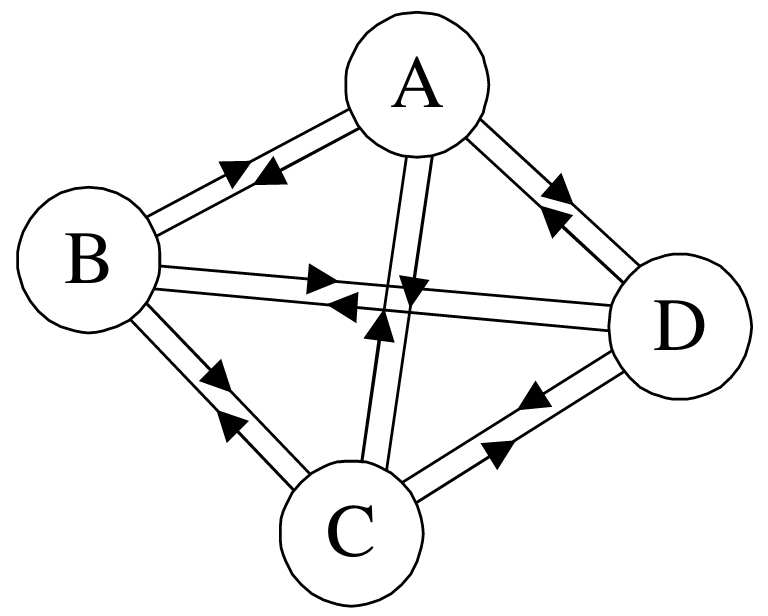
　　這里要構(gòu)造的有向帶權(quán)圖如下圖所示：

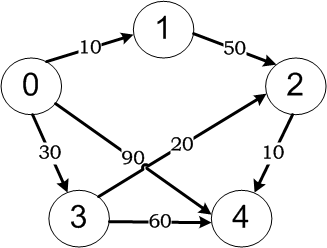
        static void DijkstraTest()
        {
            int[,] cost = new int[5, 5];
            // 初始化鄰接矩陣
            cost[0, 1] = 10;
            cost[0, 3] = 30;
            cost[0, 4] = 90;
            cost[1, 2] = 50;
            cost[2, 4] = 10;
            cost[3, 2] = 20;
            cost[3, 4] = 60;
            // 使用Dijkstra算法計(jì)算最短路徑
            Dijkstra(cost, 0);
        }

View Code

　　運(yùn)行結(jié)果如下圖所示：

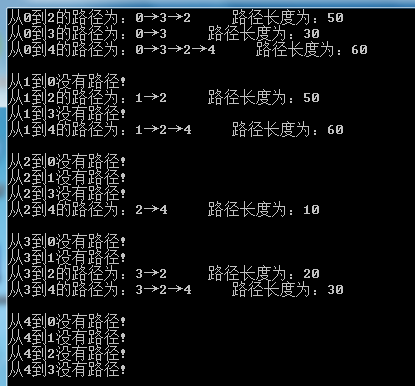
　　從圖中可以看出，從源點(diǎn)0到終點(diǎn)4的最短路徑為：0→3→2→4，該路徑長(zhǎng)度為60。

三、Floyd算法

3.1 算法思想

　　Floyd（弗洛伊德）算法提出了另外一種用于計(jì)算有向圖中所有頂點(diǎn)間的最短路徑，這種算法成為Floyd算法，它的形式較Dijkstra算法更為簡(jiǎn)單。

　　Floyd算法仍然使用鄰接矩陣存儲(chǔ)的圖，同時(shí)定義了一個(gè)二維數(shù)組A，其中每一個(gè)分量A[i,j]是頂點(diǎn)i到頂點(diǎn)j的最短路徑長(zhǎng)度。另外還使用了另一個(gè)二維數(shù)組path來(lái)保存最短路徑信息。Floyd算法的基本思想如下：

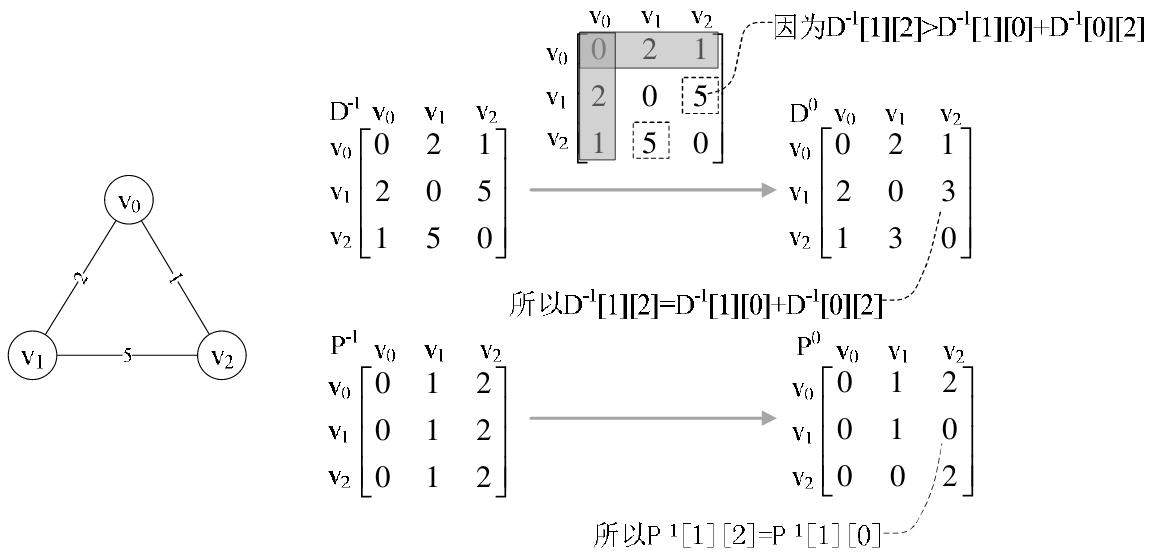
（1）初始時(shí)，對(duì)圖中任意兩個(gè)頂點(diǎn)Vi和Vj，如果從Vi到Vj存在邊，則從Vi到Vj存在一條長(zhǎng)度為cost[i,j]的路徑，但該路徑不一定是最短路徑。初始化時(shí)，A[i,j]=cost[i,j]。

（2）在圖中任意兩個(gè)頂點(diǎn)Vi和Vj之間加入頂點(diǎn)Vk，如果Vi經(jīng)Vk到達(dá)Vj的路徑存在并更短，則用A[i,k]+A[k,j]的值代替原來(lái)的A[i,j]值。

（3）重復(fù)步驟（2），直到將所有頂點(diǎn)作為中間點(diǎn)依次加入集合中，并通過(guò)迭代公式不斷修正A[i,j]的值，最終獲得任意頂點(diǎn)的最短路徑長(zhǎng)度。

3.2 算法實(shí)現(xiàn)

　　（1）代碼實(shí)現(xiàn)

        static void Floyd(int[,] cost, int v)
        {
            int n = cost.GetLength(1);  // 獲取頂點(diǎn)個(gè)數(shù)
            int[,] A = new int[n, n];   // 存放最短路徑長(zhǎng)度
            int[,] path = new int[n, n];// 存放最短路徑信息

            for (int i = 0; i < n; i++)
            {
                for (int j = 0; j < n; j++)
                {
                    // 輔助數(shù)組A和path的初始化
                    A[i, j] = cost[i, j];
                    path[i, j] = -1;
                }
            }

            // Flyod算法核心代碼部分
            for (int k = 0; k < n; k++)
            {
                for (int i = 0; i < n; i++)
                {
                    for (int j = 0; j < n; j++)
                    {
                        // 如果存在中間頂點(diǎn)K的路徑
                        if (i != j && A[i, k] != 0 && A[k, j] != 0)
                        {
                            // 如果加入中間頂點(diǎn)k后的路徑更短
                            if (A[i, j] == 0 || A[i, j] > A[i, k] + A[k, j])
                            {
                                // 使用新路徑代替原路徑
                                A[i, j] = A[i, k] + A[k, j];
                                path[i, j] = k;
                            }
                        }
                    }
                }
            }

            // 打印最短路徑及路徑長(zhǎng)度
            for (int i = 0; i < n; i++)
            {
                for (int j = 0; j < n; j++)
                {
                    if (A[i, j] == 0)
                    {
                        if (i != j)
                        {
                            Console.WriteLine("從{0}到{1}沒(méi)有路徑!", i, j);
                        }
                    }
                    else
                    {
                        Console.Write("從{0}到{1}的路徑為：", i, j);
                        Console.Write(i + "→");
                        // 使用遞歸獲取指定頂點(diǎn)的路徑
                        GetPath(path, i, j);
                        Console.Write(j + "     ");
                        Console.WriteLine("路徑長(zhǎng)度為：{0}", A[i, j]);
                    }
                }
                Console.WriteLine();
            }
        }

        static void GetPath(int[,] path, int i, int j)
        {
            int k = path[i, j];
            if (k == -1)
            {
                return;
            }

            GetPath(path, i, k);
            Console.Write(k + "→");
            GetPath(path, k, j);
        }

　　（2）基本測(cè)試

        static void FloydTest()
        {
            int[,] cost = new int[5, 5];
            // 初始化鄰接矩陣
            cost[0, 1] = 10;
            cost[0, 3] = 30;
            cost[0, 4] = 90;
            cost[1, 2] = 50;
            cost[2, 4] = 10;
            cost[3, 2] = 20;
            cost[3, 4] = 60;
            // 使用Flyod算法計(jì)算最短路徑
            Floyd(cost, 0);
        }